Cho các số phức z, w, u thỏa mãn |z - 4 + 2i| = |2z + z liên hợp| , (w-8-10i)/(w - 6 - 10i) là số thuần ảo và |u + 1 - 2i|=|u - 2 + i|.

A. (0;5]

B. (5;8)

C. [8;10)

D. $\left[10;+\infty \right)$

Trả lời

Đáp án đúng là: B

Đầu tiên ta gọi $A,N_1,M$ lần lượt là các điểm biểu diễn số phức z, w, u trên mặt phẳng tọa độ Oxy.

Khi đó ta có:$\left\{\begin{array}{l}A\left(a;b\right):\left|z-4+2i\right|=\left|2z+\overline{z}\right|\\ M\left(c;d\right):\left|u+1-2i\right|=\left|u-2+i\right|\end{array}\right.\iff \left\{\begin{array}{l}A\in \left(P\right):y=2x^2+2x-5\\ M\in \left(d\right):y=x\end{array}\right.$

Đặt $w=x+yi\left(x,y\in ℝ\right)$, khi đó

$e=\frac{w-8-10i}{w-6-10i}=k{i}^{}\left(k\in ℝ\right)\iff \left(w-8-10i\right)\overline{\left(w-6-10i\right)}=m{i}^{}\left(m\in ℝ\right)$

$\Rightarrow \left(w-8-10i\right)\left(\overline{w}-6+10i\right)={\left|w\right|}^2+\left(-6+10i\right)w-\left(8+10i\right)\overline{w}+148-20i$ (2)

Thế $w=x+yi\left(x,y\in ℝ\right)$ vào (2) kết hợp biến đổi đại số, ta được $\mathrm{Re}\left(e\right)=x^2-14x+y^2-20y+148=0$.

Suy ra $N\in \left(C\right):{\left(x-7\right)}^2+{\left(y-10\right)}^2=1$, tức $N_1$ thuộc đường tròn tâm $I_1\left(7;10\right)$, bán kính R = 1.

Khi đó ta luôn có: $P=\left|u-z\right|+\left|\overline{u-w}\right|=\left|u-z\right|+\left|u-w\right|=MA+M{N}_1\ge MA+M{I}_1-1$

Gọi $I_2$ là điểm đối xứng với $I_1\left(7;10\right)$ qua (d), khi đó ta suy ra $I_2\left(10;7\right)$ tức $N_2\in \left(I_2;1\right)$.

Khi đó ta có hình vẽ như sau:

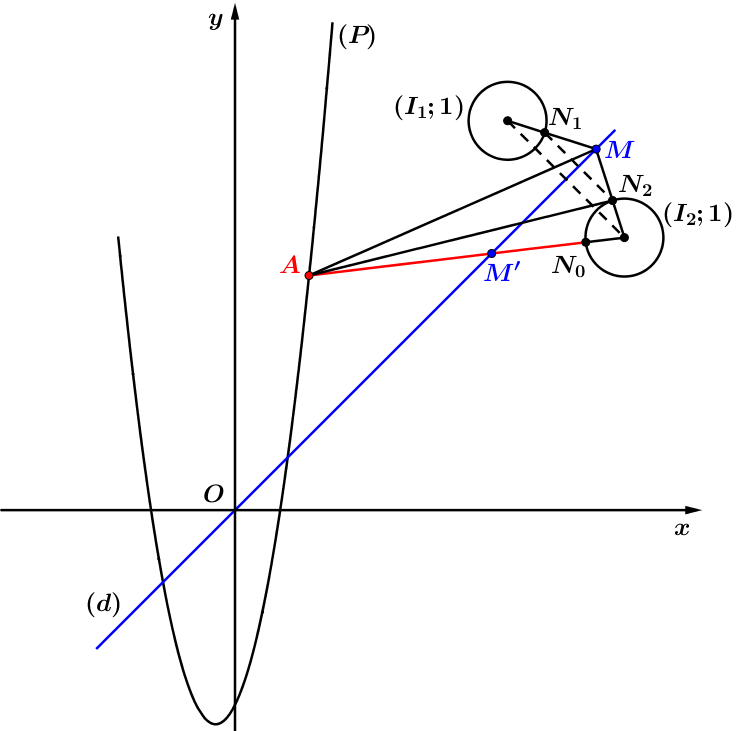
Từ hình vẽ, ta dễ dàng suy ra: $P=MA+M{I}_1-1=MA+M{I}_2-1=MA+M{N}_2$

Mặt khác theo bất đẳng thức đường gấp khúc ta luôn có: $MA+M{N}_2\ge A{N}_2$ nên $P\ge A{N}_2=A{I}_2-1$ khi $N_2\equiv N_0$ tức $P_{\min }$ khi và chỉ khi $A{I}_2$ min. Lúc này ta quy về bài toán đơn giản hơn như sau:

“Cho $A\left(a;b\right)\in \left(P\right):y=2x^2+2x-5$ và $I_2\left(10;7\right)$, khi ấy tìm giá trị nhỏ nhất của đoạn thẳng $A{I}_2$”.

Lúc này ta có: $A{I}_2=\sqrt{{\left(a-10\right)}^2+{\left(2a^2+2a-5-7\right)}^2}=\sqrt{{\left(a-10\right)}^2+4{\left(a^2+a-6\right)}^2}$.

Chạy TABLE ta suy ra $A{I}_2\ge \sqrt{63.85}-1\in \left(5;8\right)$.