Trong không gian Oxyz, cho điểm A(0;1;2) và đường thẳng d: (x-4)/2 = (y-2)/-1 = (z-1)/-2. Gọi (P) là mặt phẳng chứa d

A. $\frac{2}{3}$

B. $\frac{7}{3}$

C. $\frac{1}{3}$

D. 1

Trả lời

Đáp án đúng là: A

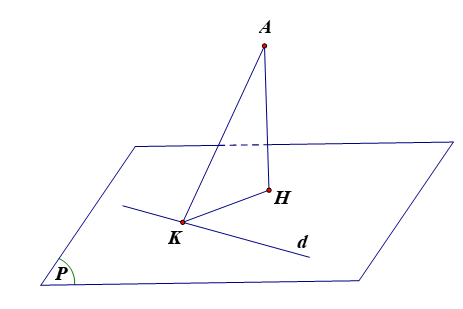
Gọi khoảng cách từ A tới mặt phẳng (P) là AH, khoảng cách từ A tới đường thẳng d là AK không đổi.

Nhận xét $AH\le AK$; Dấu "=" xảy ra $\iff H\equiv K$.

Khi đó AK vuông góc mặt phẳng (P) tại K.

Mặt phẳng (AHK) có vectơ pháp tuyến $\overrightarrow{n}=\overrightarrow{u_d}=\left(2;-1;-2\right)$ và đi qua A(0;1;2) có phương trình là 2x - y - 2z + 5 = 0.

Thế $\left\{\begin{array}{l}x=4+2t\\ y=2-t\\ z=1-2t\end{array}\right.$ vào $2x-y-2z+5=0\Rightarrow 2\left(4+2t\right)-2+t-2\left(1-2t\right)+5=0\iff t=-1$

Suy ra K(2;3;3).

Mặt phẳng (P) có vectơ pháp tuyến $\overrightarrow{n}=\overrightarrow{AK}=\left(2;2;1\right)$ và đi qua K(2;3;3) có phương trình là $2x+2y+z-13=0$.

Vậy $d\left[M;\left(P\right)\right]=\frac{\left|2.5+2\left(-1\right)+3-13\right|}{\sqrt{2^2+2^2+1^2}}=\frac{2}{3}$.