Cho hàm số $f\left(x\right)={\left(x-3\right)}^2{\left(2x-7\right)}^3{\left(3x-10\right)}^{2023}{\left(x-4\right)}^{2024}$. Biết rằng tập hợp tất cả các giá trị thực của tham số m để hàm số $h\left(x\right)=f\left(\left|-x^4+8x^2+mx\right|\right)$ có số điểm cực tiểu nhiều nhất là $S=\left(a;b\right)\backslash \left\{c\right\}$. Giá trị của biểu thức $T=a^2-ab+b^2+abc$ thuộc khoảng nào sau đây?

Đáp án đúng là: B

Trường hợp 1: f(x) = 0 thì ta thu được các nghiệm bội lẻ lần lượt là $x=\frac{7}{2};x=\frac{10}{3}$ (1)

Trường hợp 2: $f\left(x\right)\ne 0$, thực hiện biến đổi

$\left\{\begin{array}{l}\ln f\left(x\right)=2\ln \left|x-3\right|+3\ln \left|2x-7\right|+2023\ln \left|3x-10\right|+2024\ln \left|x-4\right|\\ x\in ℝ\backslash \left\{3;\frac{10}{3};\frac{7}{2};4\right\}\end{array}\right.$

Đạo hàm hai vế ta có: $\frac{f^{\text{'}}\left(x\right)}{f\left(x\right)}=\frac{2}{x-3}+\frac{6}{2x-7}+\frac{6069}{3x-10}+\frac{2024}{x-4}$

$\Rightarrow f^{\text{'}}\left(x\right)=f\left(x\right)\left(\frac{2}{x-3}+\frac{6}{2x-7}+\frac{6069}{3x-10}+\frac{2024}{x-4}\right)$

Ta giải:$f^{\text{'}}\left(x\right)=0\iff f\left(x\right)\left(\frac{2}{x-3}+\frac{6}{2x-7}+\frac{6069}{3x-10}+\frac{2024}{x-4}\right)=0$

$\iff \left[\begin{array}{l}f\left(x\right)={0^{}}^{}\left(L\right)\\ \frac{2}{x-3}+\frac{6}{2x-7}+\frac{6069}{3x-10}+\frac{2024}{x-4}={0^{}}^{}\left(2\right)\end{array}\right.$

Xét hàm số $u\left(x\right)=\frac{2}{x-3}+\frac{6}{2x-7}+\frac{6069}{3x-10}+\frac{2024}{x-4}$ có:

$u^{\text{'}}\left(x\right)=-\frac{2}{{\left(x-3\right)}^2}-\frac{12}{{\left(2x-7\right)}^2}-\frac{3.6069}{{\left(3x-10\right)}^2}-\frac{2024}{{\left(x-4\right)}^2}<0$

Suy ra $u\left(x\right)$ luôn nghịch biến trên từng khoảng xác định.

Với $\underset{x\to \pm \infty }{\lim }f\left(x\right)=0$, khi đó ta có bảng biến thiên sau:

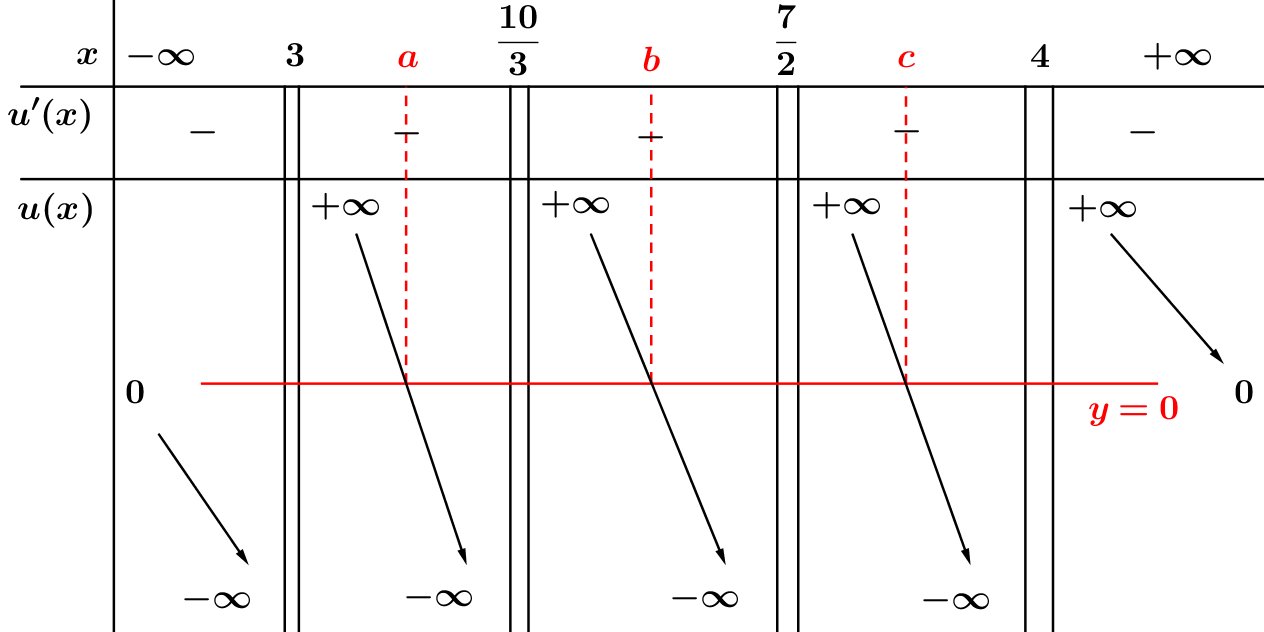
Khi đó (2) có các nghiệm là: $x=a\in \left(3;\frac{10}{3}\right);x=b\in \left(\frac{10}{3};\frac{7}{2}\right);x=c\in \left(\frac{7}{2};4\right)$ (3).

Từ (1) và (3), ta suy ra f(x) có 5 điểm cực trị lần lượt là $a,\frac{7}{2},b,\frac{10}{3},c$

(với $3<a<\frac{7}{2}<b<\frac{10}{3}<c<4$).

Tiếp đến ta xét hàm số $h\left(x\right)=f\left(\left|-x^4+8x^2+mx\right|\right)$ có

$h^{\text{'}}\left(x\right)=\frac{\left(-4x^3+16x+m\right)\left(-x^4+8x^2+mx\right)f^{\text{'}}\left(\left|-x^4+8x^2+mx\right|\right)}{\left|-x^4+8x^2+mx\right|}=0$

$\iff \left[\begin{array}{l}-4x^3+16x+m={0^{}}^{}\left(4\right)\\ -x^4+8x^2+mx={0^{}}^{}\left(5\right)\\ f^{\text{'}}\left(\left|-x^4+8x^2+mx\right|\right)={0^{}}^{}\left(6\right)\end{array}\right.$.

Để hàm số h(x) có nhiều cực tiểu nhất thì (4), (5), (6) phải có nhiều nghiệm bội lẻ nhất.

Khi đó (4) tương đương với:

$m=4x^3-16x=q\left(x\right)\to m\in \left(q\left(\frac{2}{\sqrt{3}}\right);q\left(\frac{92}{\sqrt{3}}\right)\right)\Rightarrow m\in \left(\frac{-64}{3\sqrt{3}};\frac{64}{3\sqrt{3}}\right)$ (7).

Giải (5), khi đó phương trình tương đương với:

$\left[\begin{array}{l}x=0\\ -x^3+8x+m=0^{}\left(*\right)\end{array}\right.\left(*\right)\iff m=x^3-8x=r\left(x\right)\Rightarrow m\in \left(r\left(\frac{2\sqrt{6}}{3}\right);r\left(\frac{-2\sqrt{6}}{3}\right)\right)$ 

$\Rightarrow m\in \left(-\frac{32\sqrt{6}}{9};\frac{32\sqrt{6}}{9}\right)$ (8).

Từ (7) và (8) ta suy ra $m\in \left(-\frac{32\sqrt{6}}{9};\frac{32\sqrt{6}}{9}\right)\backslash \left\{0\right\}$. (9)

Giải (6), khi đó phương trình tương đương với:

$\left\{\begin{array}{l}\left|-x^4+8x^2+mx\right|=\frac{7}{2};\left|-x^4+8x^2+mx\right|=\frac{10}{3}\\ \left|-x^4+8x^2+mx\right|=a;\left|-x^4+8x^2+mx\right|=b;\left|-x^4+8x^2+mx\right|=c\end{array}\right.$

$\iff \left\{\begin{array}{l}-x^3+8x+m=\pm \frac{7}{2x};-x^3+8x+m=\pm \frac{10}{3x}\\ -x^3+8x+m=\pm \frac{a}{x};-x^3+8x+m=\pm \frac{b}{x};-x^3+8x+m=\pm \frac{c}{x}\end{array}\right.$.

Giả sử ta có hàm số $p\left(x\right)=-x^3+8x+m$ ta suy ra để thỏa mãn đề bài thì hàm số p(x) phải luôn cắt các đường cong $-\frac{7}{2x};-\frac{10}{3x};-\frac{a}{x};-\frac{b}{x};-\frac{c}{x}$ tại 2 điểm phân biệt tại mỗi đường.

Do $c\approx \mathrm{3,6667}$ (sai số rất nhỏ) nên ta xem như $c=\frac{7}{2}=\mathrm{3,5}$.

Gọi $x_0$ là hoành độ của điểm tiếp xúc giữa p(x) và $y=\frac{7}{2x}$.

Khi đó $x_0$ là nghiệm của hệ:

$\left\{\begin{array}{l}-{x_0}^3+8x_0+m=\frac{7}{2x_0}\\ -3{x_0}^2+8=-\frac{7}{2{x_0}^2}\end{array}\right.\iff \left\{\begin{array}{l}-{x_0}^3+8x+m=\frac{7}{2x_0}\\ 6{x_0}^4-16{x_0}^2-7=0\end{array}\right.\iff \left\{\begin{array}{l}-{x_0}^3+8x_0+m=\frac{7}{2x_0}\\ x_0=\pm \mathrm{1,75}\end{array}\right.$

Suy ra: $-{\left(\pm \mathrm{1,75}\right)}^3+8\left(\pm \mathrm{1,75}\right)+m=\frac{7}{2\left(\pm \mathrm{1,75}\right)}\iff m=\pm \mathrm{6,64}$.

Như vậy để thỏa mãn yêu cầu đề bài thì ta cần có $m\in \left(-\mathrm{6,64};\mathrm{6,64}\right)$ (10).

Từ (9) và (10) ta suy ra $m\in \left(-\mathrm{6,64};\mathrm{6,64}\right)\backslash \left\{0\right\}$.