Trong không gian Oxyz, cho ba đường thẳng $d_1:\frac{x-1}{2}=\frac{y-1}{1}=\frac{z-1}{-2},$ $d_2:\frac{x-3}{1}=\frac{y+1}{2}=\frac{z-2}{2},$$d_3:\frac{x-4}{2}=\frac{y-4}{-2}=\frac{z-1}{1}$. Mặt cầu bán kính nhỏ nhất tâm I(a;b;c), tiếp xúc với 3 đường thẳng $d_1,d_2,d_3$. Giá trị tổng $S=a+2b+3c$ là

Đáp án đúng là: A

$d_1$ đi qua điểm A(1;1;1) có $VTCP\overrightarrow{u_1}=\left(2;1;-2\right)$.

$d_2$ đi qua điểm B(3;-1;2) có $VTCP\overrightarrow{u_2}=\left(1;2;2\right)$.

$d_3$ đi qua điểm C(4;4;1) có $VTCP\overrightarrow{u_3}=(2;-2;1)$.

Ta có: $\overrightarrow{u_1}.\overrightarrow{u_2}=\mathrm{0,}\overrightarrow{u_2}.\overrightarrow{u_3}=\mathrm{0,}\overrightarrow{u_3}.\overrightarrow{u_1}=0\Rightarrow \left(d_1\right),\left(d_2\right),\left(d_3\right)$ đôi một vuông góc với nhau.

$\left[\overrightarrow{u_1};\overrightarrow{u_2}\right].\overrightarrow{AB}\ne \mathrm{0,}\left[\overrightarrow{u_2};\overrightarrow{u_3}\right].\overrightarrow{BC}\ne \mathrm{0,}\left[\overrightarrow{u_3},\overrightarrow{u_1}\right].\overrightarrow{CA}\ne 0\Rightarrow \left(d_1\right),\left(d_2\right),\left(d_3\right)$ đôi một chéo nhau.

Lại có: $\overrightarrow{AB}=\left(2;-2;1\right);\overrightarrow{AB}.\overrightarrow{u_1}=0$ và $\overrightarrow{AB}.\overrightarrow{u_2}=0$ nên $\left(d_1\right),\left(d_2\right),\left(d_3\right)$ chứa 3 cạnh của hình hộp chữ nhật như hình vẽ.

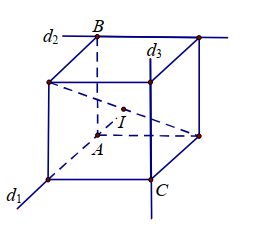
Vì mặt cầu tâm $I(a;b;c)$ tiếp xúc với 3 đường thẳng $\left(d_1\right),\left(d_2\right),\left(d_3\right)$ nên bán kính

$R=d\left(I,d_1\right)=d\left(I,d_2\right)=d\left(I,d_3\right)\iff R^2=d^2\left(I,d_1\right)=d^2\left(I,d_2\right)=d^2\left(I,d_3\right)$

$\iff R^2={\left(\frac{\left|\left[\overrightarrow{AI},{\overrightarrow{u}}_1\right]\right|}{\left|\overrightarrow{u_1}\right|}\right)}^2={\left(\frac{\left|\left[\overrightarrow{BI},\overrightarrow{u_2}\right]\right|}{\left|\overrightarrow{u_2}\right|}\right)}^2={\left(\frac{\left|\left[\overrightarrow{CI},\overrightarrow{u_3}\right]\right|}{\left|\overline{u_3}\right|}\right)}^2$, ta thấy ${\left|\overrightarrow{u_1}\right|}^2={\left|\overrightarrow{u_2}\right|}^2={\left|\overrightarrow{u_3}\right|}^2=9$ và

$\overrightarrow{AI}=\left(a-1;b-1;c-1\right),\left[\overrightarrow{AI},\overrightarrow{u_1}\right]=\left(-2b-c+3;2a+2c-4;a-2b+1\right)$.

$\overrightarrow{BI}=\left(a-3;b+1;c-2\right),\left[\overrightarrow{BI},\overrightarrow{u_2}\right]=\left(2b-2c+6;-2a+c+4;2a-b-7\right).$

$\overrightarrow{CI}=\left(a-4;b-4;c-1\right),\left[\overrightarrow{CI},\overrightarrow{u_3}\right]=\left(b+2c-6;-a+2c+2;-2a-2b+16\right).$

$9R^2={\left|\left[\overrightarrow{AI},{\overrightarrow{u}}_1\right]\right|}^2={\left|\left[\overrightarrow{BI},\overrightarrow{u_2}\right]\right|}^2={\left|\left[\overrightarrow{CI},\overrightarrow{u_3}\right]\right|}^2\Rightarrow 27R^2={\left|\left[\overrightarrow{AI},{\overrightarrow{u}}_1\right]\right|}^2+{\left|\left[\overrightarrow{BI},\overrightarrow{u_2}\right]\right|}^2+{\left|\left[\overrightarrow{CI},\overrightarrow{u_3}\right]\right|}^2$

$=18\left(a^2+b^2+c^2\right)-126a-54b-54c+423$

$=18{\left(a-\frac{7}{2}\right)}^2+18{\left(b-\frac{3}{2}\right)}^2+18{\left(c-\frac{3}{2}\right)}^2+\frac{243}{2}\ge \frac{243}{2}$

$\Rightarrow R_{\min }=\frac{3\sqrt{2}}{2}\approx \mathrm{2,12}$ khi $a=\frac{7}{2},b=\frac{3}{2},c=\frac{3}{2}$.

Tổng $S=a+2b+3c=11$.