Cho hai số phức z1, z2 thoả mãn đồng thời hai điều kiện sau |z - 1|= căn 34, |z+1+mi|=|z+m + 2i| (trong đó m là tham số thực)
A. √34
B. 2√34
C. 10
D. 2
A. √34
B. 2√34
C. 10
D. 2
Đáp án đúng là: D
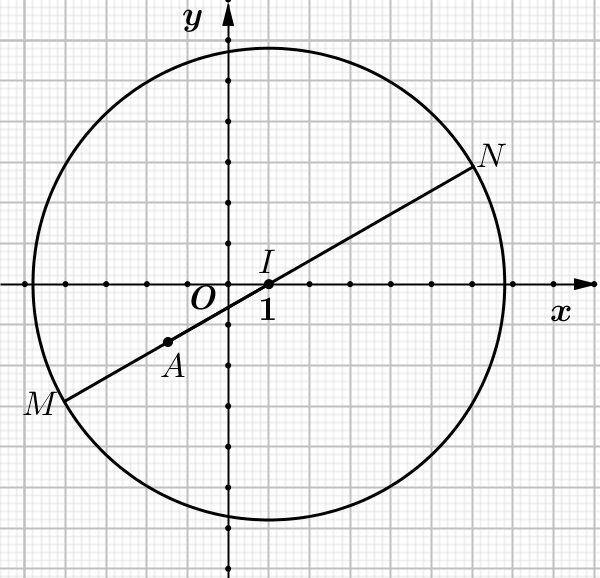
Đặt z=x+yi (x, y∈ℝ). Khi đó |z−1|=√34⇔(x−1)2+y2=34 (C).
Suy ra điểm biểu diễn của số phức z1, z2 nằm trên đường tròn (C) tâm I(1;0) bán kính R=√34.
Lại có, |z+1+mi|=|z+m+2i|⇔(x+1)2+(y+m)2=(x+m)2+(y+2)2
⇔(2−2m)x+(2m−4)y−3=0 (d).
Suy ra điểm biểu diễn số phức z1, z2 nằm trên đường thẳng (d).
Gọi A(x0; y0) là điểm cố định mà đường thẳng (d) luôn đi qua. Khi đó, (2−2m)x0+(2m−4)y0−3=0, ∀m
⇔ 2m(y0−x0)+2x0−4y0−3=0, ∀m
⇔ {y0−x0=02x0−4y0−3=0⇔x0=y0=−32⇒A(−32; −32).
Ta có, IA=√342<R nên điểm A nằm trong đường tròn (C).
Do đó đường thẳng (d) luôn cắt đường tròn (C) tại 2 điểm M, N và điểm M, N chính là điểm biểu diễn của số phức z1, z2.
Theo giả thiết thì |z1−z2|=MN lớn nhất ⇔ (d)≡ ![]()
![]() .
.
Do đó .