Trên đường tròn lượng giác, xác định điểm M biểu diễn các góc lượng giác có số đo sau và tính các giá trị lượng giác của chúng. a) 23pi /4 b) 31pi /6 c) – 1 380°.
43
08/09/2024
Trên đường tròn lượng giác, xác định điểm M biểu diễn các góc lượng giác có số đo sau và tính các giá trị lượng giác của chúng.
a) 23π4; b) 31π6; c) – 1 380°.
Trả lời
Lời giải
a) Ta có 23π4=6π−π4. Góc 23π4 được biểu diễn bởi điểm M(√22;−√22) trên đường tròn lượng giác (hình dưới).
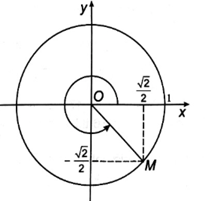
Vậy sin23π4=−√22;cos23π4=√22 và tan23π4=cot23π4=−1.
b) Ta có 31π6=7π6+4π. Góс 31π6 được biểu diễn bởi điểm M(−√32;−12) trên đường tròn lượng giác (hình dưới).
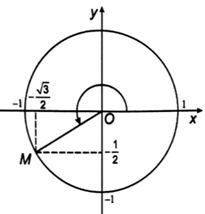
Vậy sin31π6=−12;cos31π6=−√32; tan31π6=1√3 và cot31π6=√3.
c) Ta có – 1 380° = − 4 . 360° + 60°. Góc –1 380° được biểu diễn bởi điểm M(12;√32) trên đường tròn lượng giác (hình dưới).
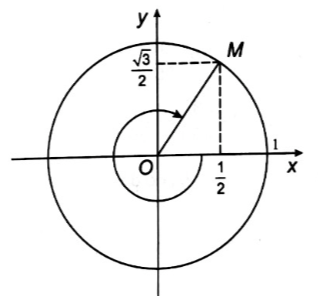
Vậy sin(– 1 380°) = √32; cos(– 1 380°) = 12; tan(– 1 380°) = √3 và cot(– 1 380°) = 1√3.



