Tìm giá trị lớn nhất và giá trị nhỏ nhất của p

a) y = sin x – cos x;

b) y = sin x + sin\(\left( {\frac{\pi }{3} - x} \right)\);

c) y = sin⁴ x + cos⁴ x;

d) y = cos 2x + 2cos x – 1.

Lời giải

a) Ta có y = sin x – cos x = \(\sqrt 2 \sin \left( {x - \frac{\pi }{4}} \right)\).

Vì \( - 1 \le \sin \left( {x - \frac{\pi }{4}} \right) \le 1\) nên \( - \sqrt 2 \le \sqrt 2 \sin \left( {x - \frac{\pi }{4}} \right) \le \sqrt 2 \), với mọi \(x \in \mathbb{R}\).

Vậy giá trị lớn nhất của hàm số là \(\sqrt 2 \), đạt được khi \(\sin \left( {x - \frac{\pi }{4}} \right) = 1\)

\( \Leftrightarrow x - \frac{\pi }{4} = \frac{\pi }{2} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\) \( \Leftrightarrow x = \frac{{3\pi }}{4} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\).

Giá trị nhỏ nhất của hàm số là \( - \sqrt 2 \), đạt được khi \(\sin \left( {x - \frac{\pi }{4}} \right) = - 1\)

\( \Leftrightarrow x - \frac{\pi }{4} = - \frac{\pi }{2} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\) \( \Leftrightarrow x = - \frac{\pi }{4} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\).

b) Ta có y = sin x + sin\(\left( {\frac{\pi }{3} - x} \right)\) \( = 2\sin \frac{{x + \frac{\pi }{3} - x}}{2}\cos \frac{{x - \frac{\pi }{3} + x}}{2}\)

\( = 2\sin \frac{\pi }{6}\cos \left( {x - \frac{\pi }{6}} \right)\)\( = 2.\frac{1}{2}\cos \left( {x - \frac{\pi }{6}} \right) = \cos \left( {x - \frac{\pi }{6}} \right)\).

Ta có \( - 1 \le \cos \left( {x - \frac{\pi }{6}} \right) \le 1\,\,\forall x \in \mathbb{R}\).

Vậy giá trị lớn nhất của hàm số là 1, đạt được khi \(\cos \left( {x - \frac{\pi }{6}} \right) = 1\)\( \Leftrightarrow x - \frac{\pi }{6} = k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\)\( \Leftrightarrow x = \frac{\pi }{6} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\) và giá trị nhỏ nhất của hàm số là – 1, đạt được khi \(\cos \left( {x - \frac{\pi }{6}} \right) = - 1\)\( \Leftrightarrow x - \frac{\pi }{6} = \pi + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\)\( \Leftrightarrow x = \frac{{7\pi }}{6} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\).

c) Ta có y = sin⁴ x + cos⁴ x = (sin² x + cos² x)² – 2sin² x cos² x

= 1 – 2 (sin x cos x)² = \(1 - 2.{\left( {\frac{{\sin 2x}}{2}} \right)^2}\)= \(1 - \frac{1}{2}{\sin ^2}2x\)

= \(1 - \frac{1}{2}.\frac{{1 - \cos 4x}}{2}\) = \(1 - \frac{1}{4} + \frac{1}{4}\cos 4x\) = \(\frac{3}{4} + \frac{1}{4}\cos 4x\).

Vì – 1 ≤ cos 4x ≤ 1 nên \( - \frac{1}{4} \le \frac{1}{4}\cos 4x \le \frac{1}{4}\), do đó \(\frac{3}{4} - \frac{1}{4} \le \frac{3}{4} + \frac{1}{4}\cos 4x \le \frac{3}{4} + \frac{1}{4}\)

hay \(\frac{1}{2} \le \frac{3}{4} + \frac{1}{4}\cos 4x \le 1\,\,\,\forall x \in \mathbb{R}\).

Vậy giá trị lớn nhất của hàm số là 1, đạt được khi cos 4x = 1 ⇔ 4x = k2π (k ∈ ℤ)

\( \Leftrightarrow x = k\frac{\pi }{2}\,\,\left( {k \in \mathbb{Z}} \right)\).

Giá trị nhỏ nhất của hàm số là \(\frac{1}{2}\), đạt được khi cos 4x = – 1 ⇔ 4x = π + k2π (k ∈ ℤ)

\( \Leftrightarrow x = \frac{\pi }{4} + k\frac{\pi }{2}\,\,\left( {k \in \mathbb{Z}} \right)\).

d) Ta có y = cos 2x + 2cos x − 1

= (2cos² x – 1) + 2cos x – 1

= 2cos² x + 2cos x – 2

= 2t² + 2t – 2 với t = cos x ∈ [– 1; 1].

Xét hàm số y = 2t² + 2t – 2 trên đoạn [– 1; 1]. Hàm số này có đồ thị như trong hình vẽ dưới đây.

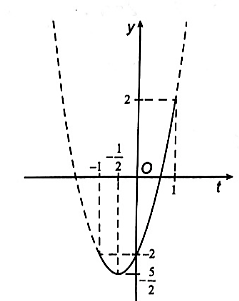
Từ đồ thị ở hình trên ta suy ra được giá trị lớn nhất của hàm số đã cho là 2, đạt được khi cos x = 1 ⇔ x = k2π (k ∈ ℤ) và giá trị nhỏ nhất của hàm số là \( - \frac{5}{2}\), đạt được khi \(\cos x = - \frac{1}{2}\)\( \Leftrightarrow x = \pm \frac{{2\pi }}{3} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\).