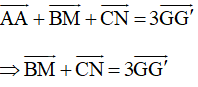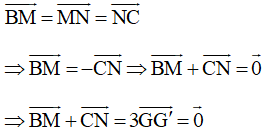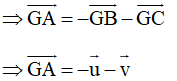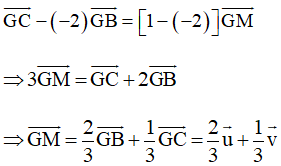Trên cạnh BC của tam giác ABC lấy các điểm M, N không trùng với B và C sao cho BM = MN =NC

Bài 4.60 trang 70 SBT Toán 10 Tập 1: Trên cạnh BC của tam giác ABC lấy các điểm M, N không trùng với B và C sao cho BM = MN =NC.

a) Chứng minh rằng hai tam giác ABC và AMN có cùng trọng tâm.

b) Gọi G là trọng tâm của tam giác ABC. Đặt $\overrightarrow{GB}=\overrightarrow{u}$và $\overrightarrow{GC}=\overrightarrow{v}.$ Hãy biểu thị các vectơ sau qua hai vectơ $\overrightarrow{u}$và $\overrightarrow{v}:$$\overrightarrow{GA},\overrightarrow{GM},\overrightarrow{GN}.$

Trả lời

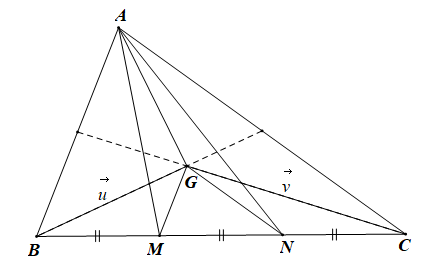
a) Giả sử G, G' lần lượt là trọng tâm của DABC, DAMN.

Sử dụng kết quả của Ví dụ 3, Bài 9 (trang 53, Sách bài tập, Toán 10, Tập một) ta có:

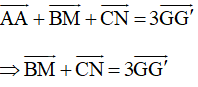
Mặt khác: M, N lần lượt lấy theo thứ tự trên cạnh BC sao cho BM = MN = NC nên ta có: 

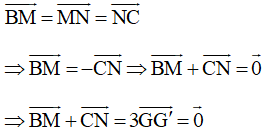
Suy ra điểm G và G' trùng nhau.

Do đó hai tam giác ABC và AMN có cùng trọng tâm.

b) • Vì G là trọng tâm của tam giác ABC nên $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$

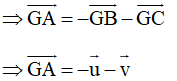
• Từ BM = MN = NC suy ra $\overrightarrow{MC}=-2\overrightarrow{MB}$

Theo Nhận xét ở Ví dụ 2, Bài 9 (trang 53, Sách bài tập, Toán 10, Tập một), với điểm G ta có:

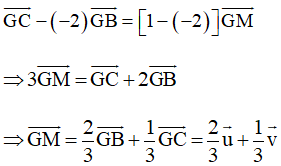
Tương tự ta cũng có: $\overrightarrow{GN}=\frac{1}{3}\overrightarrow{u}+\frac{2}{3}\overrightarrow{v}$

Xem thêm các bài giải SBT Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

Bài 10: Vectơ trong mặt phẳng tọa độ

Bài 11: Tích vô hướng của hai vectơ

Bài tập cuối chương 4

Bài 12: Số gần đúng và sai số

Bài 13: Các số đặc trưng đo xu thế trung tâm

Bài 14: Các số đặc trưng đo độ phân tán