Cho bốn điểm A, B, C, D trong mặt phẳng. Chứng minh rằng vecto AB.CD + BC.AD + CA.BD = 0

151 11/01/2024

Bài 4.66 trang 71 SBT Toán 10 Tập 1: Cho bốn điểm A, B, C, D trong mặt phẳng. Chứng minh rằng $\vec{A B} . \vec{C D} + \vec{B C} . \vec{A D} + \vec{C A} . \vec{B D} = 0.$

Trả lời

Ta có:

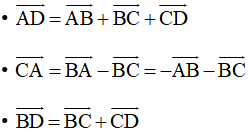
Sách bài tập Toán 10 Bài tập cuối chương 4 - Kết nối tri thức (ảnh 1)

Suy ra: $\vec{A B} . \vec{C D} + \vec{B C} . \vec{A D} + \vec{C A} . \vec{B D}$

$= \vec{A B} . \vec{C D} + \vec{B C} . (\vec{A B} + \vec{B C} + \vec{C D})$ $+ (- \vec{A B} - \vec{B C}) . (\vec{B C} + \vec{C D})$

$= \vec{A B} . \vec{C D} + \vec{B C} . \vec{A B} + {\vec{B C}}^{2} + \vec{B C} . \vec{C D} -$ $\vec{A B} . \vec{B C} - \vec{A B} . \vec{C D} - {\vec{B C}}^{2} - \vec{B C} . \vec{C D}$

= 0.

Vậy $\vec{A B} . \vec{C D} + \vec{B C} . \vec{A D} + \vec{C A} . \vec{B D} = 0.$

Xem thêm các bài giải SBT Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

Bài 10: Vectơ trong mặt phẳng tọa độ

Bài 11: Tích vô hướng của hai vectơ

Bài tập cuối chương 4

Bài 12: Số gần đúng và sai số

Bài 13: Các số đặc trưng đo xu thế trung tâm

Bài 14: Các số đặc trưng đo độ phân tán

Bài tập cuối chương 4 - kntt

Câu hỏi cùng chủ đề

Một ô tô có khối lượng 2,5 tấn chạy từ chân lên đỉnh một con dốc thẳng. Tính công của trọng lực tác động lên xe

Bài 4.70 trang 71 SBT Toán 10 Tập 1. Một ô tô có khối lượng 2,5 tấn chạy từ chân lên đỉnh một con dốc thẳng. Tính công của trọng lực tác động lên xe, biết dốc dài 50 m và nghiêng 15° so với phương nằm ngang (trong tính toán, lấy gia tốc trọng trường bằng 10 m/s²).

Bài tập cuối chương 4 - kntt

159 1 năm trước

Trong mặt phẳng toạ độ Oxy cho ba điểm A(2; −1), B(5; 3) và C(–2; 9). a) Tìm điểm D thuộc trục hoành

Bài 4.69 trang 71 SBT Toán 10 Tập 1. Trong mặt phẳng toạ độ Oxy cho ba điểm A(2; −1), B(5; 3) và C(–2; 9). a) Tìm điểm D thuộc trục hoành sao cho B, C, D thẳng hàng. b) Tìm điểm E thuộc trục hoành sao cho EA + EB nhỏ nhất. c) Tìm điểm F thuộc trục tung sao cho vectơ FA→+FB→+FC→ có độ dài ngắn nhất.

Bài tập cuối chương 4 - kntt

222 1 năm trước

Trong mặt phẳng toạ độ Oxy cho ba điểm A(–2; 1), B(1; 4) và C(5; −2). a) Chứng minh rằng A, B, C

Bài 4.68 trang 71 SBT Toán 10 Tập 1. Trong mặt phẳng toạ độ Oxy cho ba điểm A(–2; 1), B(1; 4) và C(5; −2). a) Chứng minh rằng A, B, C là ba đỉnh của một tam giác. Tìm toạ độ trọng tâm G của tam giác ABC. b) Tìm toạ độ trực tâm H và tâm đường tròn ngoại tiếp I của tam giác ABC.

Bài tập cuối chương 4 - kntt

201 1 năm trước

Trong mặt phẳng toạ độ Oxy cho ba vecto a = (1;2). b = (3;-4), c = (-5;3)

Bài 4.67 trang 71 SBT Toán 10 Tập 1. Trong mặt phẳng toạ độ Oxy cho ba a) Tính các tích vô hướng b) Tìm góc giữa hai vectơ a→ và b→+c→.

Bài tập cuối chương 4 - kntt

205 1 năm trước

Cho hình thang vuông ABCD có góc DAB = ABC = 900 độ BC = 1, AB = 2 và AD = 3. Gọi M là trung điểm

Bài 4.65 trang 70 SBT Toán 10 Tập 1. Cho hình thang vuông ABCD có DAB^=ABC^=90°,BC = 1, AB = 2 và AD = 3. Gọi M là trung điểm của AB. a) Hãy biểu thị các vectơ CM→, CM→ theo hai vectơ AB→ và AD→ b) Gọi N là trung điểm CD, G là trọng tâm tam giác MCD, và I là điểm thuộc cạnh CD sao cho 9IC = 5ID. Chứng minh rằng A, G, I thẳng hàng. c) Tính độ dài các đoạn thẳng AI và BI.

Bài tập cuối chương 4 - kntt

162 1 năm trước

Cho tứ giác lồi ABCD không có hai cạnh nào song song. Gọi E, F theo thứ tự là trung điểm AB, CD

Bài 4.64 trang 70 SBT Toán 10 Tập 1. Cho tứ giác lồi ABCD không có hai cạnh nào song song. Gọi E, F theo thứ tự là trung điểm AB, CD. Gọi K, L, M, N lần lượt là trung điểm của AF, CE, BF, DE. a) Chứng minh rằng tứ giác KLMN là một hình bình hành. b) Gọi I là giao điểm của KM, LN. Chứng minh rằng E, I, F thẳng hàng.

Bài tập cuối chương 4 - kntt

149 1 năm trước

Cho tam giác ABC với trọng tâm G. Lấy điểm A', B' sao cho vecto AA' = 2BC, BB' = 2CA Gọi G' là trọng

Bài 4.63 trang 70 SBT Toán 10 Tập 1. Cho tam giác ABC với trọng tâm G. Lấy điểm A', B' sao cho AA'→=2BC→,BB'→=2CA→. Gọi G' là trọng tâm của tam giác A'B'C. Chứng minh rằng GG' song song với AB.

Bài tập cuối chương 4 - kntt

152 1 năm trước

Cho hình bình hành ABCD. Gọi M, N theo thứ tự là trung điểm các cạnh AB, CD. Lấy P thuộc đoạn DM

Bài 4.62 trang 70 SBT Toán 10 Tập 1. Cho hình bình hành ABCD. Gọi M, N theo thứ tự là trung điểm các cạnh AB, CD. Lấy P thuộc đoạn DM và Q thuộc đoạn BN sao cho DP = 2PM, BQ = xQN. Đặt AB→=u→ và AD→=v→. a) Hãy biểu thị các vectơ AP→, AQ→ qua hai vectơ u→ và v→ b) Tìm x đề A, P, Q thằng hàng.

Bài tập cuối chương 4 - kntt

130 1 năm trước

Cho tam giác ABC có AB = 4, AC = 5 và góc CAB = 60 độ a) Tính tích vô hướng

Bài 4.61 trang 70 SBT Toán 10 Tập 1. Cho tam giác ABC có AB = 4, AC = 5 và CAB^=60°. a) Tính tích vô hướng AB→.AC→, AB→.BC→. b) Lấy các điểm M, N thoả mãn 2AM→+3MC→=0→và NB→+xNC→=0→(x ≠ –1). Xác định x sao cho AN vuông góc với BM.

Bài tập cuối chương 4 - kntt

150 1 năm trước

Trên cạnh BC của tam giác ABC lấy các điểm M, N không trùng với B và C sao cho BM = MN =NC

Bài 4.60 trang 70 SBT Toán 10 Tập 1. Trên cạnh BC của tam giác ABC lấy các điểm M, N không trùng với B và C sao cho BM = MN =NC. a) Chứng minh rằng hai tam giác ABC và AMN có cùng trọng tâm. b) Gọi G là trọng tâm của tam giác ABC. Đặt GB→=u→và GC→=v→. Hãy biểu thị các vectơ sau qua hai vectơ u→và v→.GA→, GM→, GN→.

Bài tập cuối chương 4 - kntt

165 1 năm trước

Xem tất cả

Cho bốn điểm A, B, C, D trong mặt phẳng. Chứng minh rằng vecto AB.CD + BC.AD + CA.BD = 0

Trả lời

Câu hỏi cùng chủ đề

Một ô tô có khối lượng 2,5 tấn chạy từ chân lên đỉnh một con dốc thẳng. Tính công của trọng lực tác động lên xe

Trong mặt phẳng toạ độ Oxy cho ba điểm A(2; −1), B(5; 3) và C(–2; 9). a) Tìm điểm D thuộc trục hoành

Trong mặt phẳng toạ độ Oxy cho ba điểm A(–2; 1), B(1; 4) và C(5; −2). a) Chứng minh rằng A, B, C

Trong mặt phẳng toạ độ Oxy cho ba vecto a = (1;2). b = (3;-4), c = (-5;3)

Cho hình thang vuông ABCD có góc DAB = ABC = 900 độ BC = 1, AB = 2 và AD = 3. Gọi M là trung điểm

Cho tứ giác lồi ABCD không có hai cạnh nào song song. Gọi E, F theo thứ tự là trung điểm AB, CD

Cho tam giác ABC với trọng tâm G. Lấy điểm A', B' sao cho vecto AA' = 2BC, BB' = 2CA Gọi G' là trọng

Cho hình bình hành ABCD. Gọi M, N theo thứ tự là trung điểm các cạnh AB, CD. Lấy P thuộc đoạn DM

Cho tam giác ABC có AB = 4, AC = 5 và góc CAB = 60 độ a) Tính tích vô hướng

Trên cạnh BC của tam giác ABC lấy các điểm M, N không trùng với B và C sao cho BM = MN =NC

Danh mục