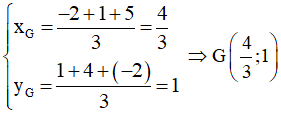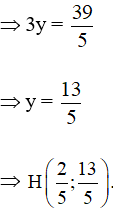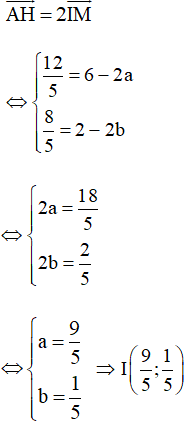Trong mặt phẳng toạ độ Oxy cho ba điểm A(–2; 1), B(1; 4) và C(5; −2). a) Chứng minh rằng A, B, C

Bài 4.68 trang 71 SBT Toán 10 Tập 1: Trong mặt phẳng toạ độ Oxy cho ba điểm A(–2; 1), B(1; 4) và C(5; −2).

a) Chứng minh rằng A, B, C là ba đỉnh của một tam giác. Tìm toạ độ trọng tâm G của tam giác ABC.

b) Tìm toạ độ trực tâm H và tâm đường tròn ngoại tiếp I của tam giác ABC.

Trả lời

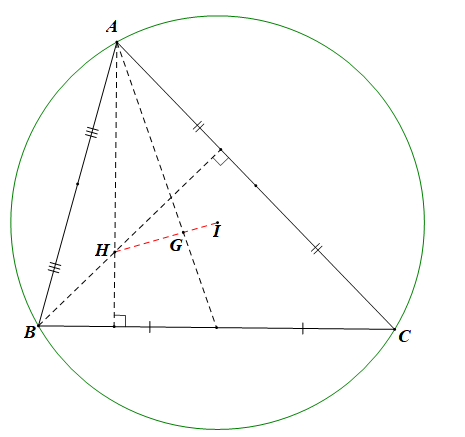
a) Với A(–2; 1), B(1; 4) và C(5; −2) ta có:

$\overrightarrow{AB}$ = (3; 3) và $\overrightarrow{AC}$ = (7; –3)

Vì $\frac{3}{7}\ne \frac{3}{-3}=-1$ nên hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{AC}$ không cùng phương

Do đó ba điểm A, B, C không thẳng hàng

Vậy A, B, C là ba đỉnh của một tam giác.

Vì G là trọng tâm của tam giác ABC nên ta có:

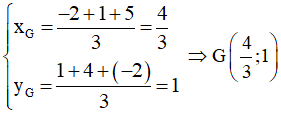
Vậy tọa độ trọng tâm của tam giác ABC là: $G\left(\frac{4}{3};1\right)$.

b) *Tìm tọa độ trực tâm H của tam giác ABC:

Vì H là trực tâm của tam giác ABC nên AH ⊥ BC và BH ⊥ AC

Hay $\overrightarrow{AH}.\overrightarrow{BC}=0$ và $\overrightarrow{BH}.\overrightarrow{AC}=0$ 

Giả sử H(x; y) là tọa độ trực tâm tam giác ABC

Với A(–2; 1), B(1; 4), C(5; −2) và H(x; y) ta có:

• $\overrightarrow{AH}$ = (x + 2; y – 1) và $\overrightarrow{BC}$ = (4; –6)

$\Rightarrow \overrightarrow{AH}.\overrightarrow{BC}$ = 4.(x + 2) – 6.(y – 1) = 0

$\Rightarrow$ 4x – 6y = –14

$\Rightarrow$ 2x – 3y = –7     (1)

• $\overrightarrow{BH}$ = (x – 1; y – 4) và $\overrightarrow{AC}$ = (7; –3)

$\Rightarrow \overrightarrow{BH}.\overrightarrow{AC}$ = 7.(x – 1) – 3.(y – 4) = 0

$\Rightarrow$ 7x – 3y = –5     (2)

Trừ vế theo vế (2) cho (1) ta có: 5x = 2

$\Rightarrow$ x = $\frac{2}{5}$

Thay x = $\frac{2}{5}$ vào (1) ta được:  2.$\frac{2}{5}$ – 3y =  –7

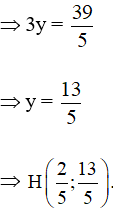
Vậy tọa độ trực tâm của tam giác ABC là $H\left(\frac{2}{5};\frac{13}{5}\right).$

* Tìm tọa độ tâm I của đường tròn ngoại tiếp tam giác ABC:

Theo kết quả phần a) của Bài 4.15, trang 54, Sách Bài tập, Toán 10, tập một ta có:

$\overrightarrow{AH}=2\overrightarrow{IM}$ với M là trung điểm của BC.

Giả sử I(a; b) là tọa độ tâm đường tròn ngoại tiếp tam giác ABC

Với A(–2; 1), B(1; 4), C(5; −2), $H\left(\frac{2}{5};\frac{13}{5}\right)$ và I(a; b) ta có:

• $\overrightarrow{AH}=\left(\frac{12}{5};\frac{8}{5}\right)$

• M là trung điểm của BC nên $\left\{\begin{array}{l}{x}_M=\frac{1+5}{2}=3\\ y_M=\frac{4+\left(-2\right)}{2}=1\end{array}\right.$

$\Rightarrow$ M(3; 1)

$\Rightarrow \overrightarrow{IM}$ = (3 – a; 1 – b)

$\Rightarrow 2\overrightarrow{IM}$ = (6 – 2a; 2 – 2b)

Ta có 

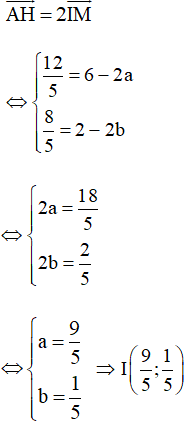
Vậy tọa độ tâm đường tròn ngoại tiếp tam giác ABC là $I\left(\frac{9}{5};\frac{1}{5}\right).$

Xem thêm các bài giải SBT Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

Bài 10: Vectơ trong mặt phẳng tọa độ

Bài 11: Tích vô hướng của hai vectơ

Bài tập cuối chương 4

Bài 12: Số gần đúng và sai số

Bài 13: Các số đặc trưng đo xu thế trung tâm

Bài 14: Các số đặc trưng đo độ phân tán