Cho tứ giác lồi ABCD không có hai cạnh nào song song. Gọi E, F theo thứ tự là trung điểm AB, CD
136
11/01/2024
Bài 4.64 trang 70 SBT Toán 10 Tập 1: Cho tứ giác lồi ABCD không có hai cạnh nào song song. Gọi E, F theo thứ tự là trung điểm AB, CD. Gọi K, L, M, N lần lượt là trung điểm của AF, CE, BF, DE.
a) Chứng minh rằng tứ giác KLMN là một hình bình hành.
b) Gọi I là giao điểm của KM, LN. Chứng minh rằng E, I, F thẳng hàng.
Trả lời
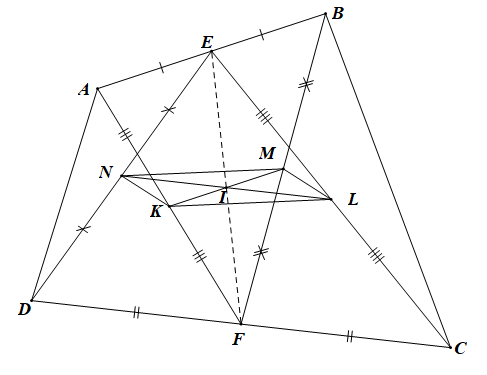
F là trung điểm của CD Fnên
• Vì K là trung điểm của AF, L là trung điểm của CE, theo kết quả của Bài tập 4.12, trang 58, Toán 10, Tập một, ta có:
Tương tự:
M là trung điểm của BF, N là trung điểm của DE, nên ta có:
Do đó
KL = NM và KL // NM
KLMN là một hình bình hành.
b) Do KLMN là hình bình hành
Mà I là giao điểm của KM, LN nên I là trung điểm chung của KM, LN.
Khi đó ta có:
(do F là trung điểm của DC)
Do đó
Suy ra hai vectơ và cùng phương
Do đó E, I, F thẳng hàng.
Xem thêm các bài giải SBT Toán lớp 10 Kết nối tri thức hay, chi tiết khác:
Bài 10: Vectơ trong mặt phẳng tọa độ
Bài 11: Tích vô hướng của hai vectơ
Bài tập cuối chương 4
Bài 12: Số gần đúng và sai số
Bài 13: Các số đặc trưng đo xu thế trung tâm
Bài 14: Các số đặc trưng đo độ phân tán

