Tính thể tích của khối chóp SABC có AB=a, AC=2a, góc BAC=120 ( SAB) và ( SAC) cùng vuông góc với ( ABC)
Tính thể tích của khối chóp SABC có AB=a, AC=2a, ( SAB) và ( SAC) cùng vuông góc với ( ABC), góc giữa mặt phẳng và là
A.
B.
C.
D.
A.
B.
C.
D.
Chọn C
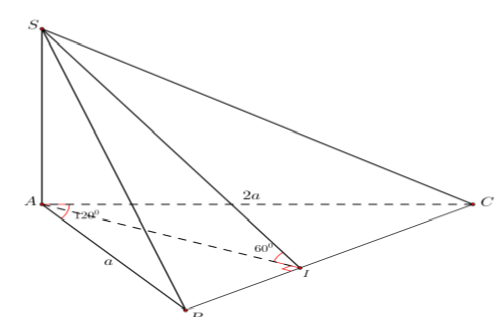
Ta có
Trong mặt phẳng kẻ
Suy ra góc giữa 2 mặt phẳng
Trong tam giác ABC ta có
Ta có
Mà
Trong tam giác vuông tại A ta có
Vậy thể tích của khối chóp là