Tìm tất cả các giá trị của tham số m để đồ thị hàm số y=x−1√2x2−2x−m−x−1 có đúng bốn đường tiệm cận.
A. m∈[−5; 4]\{−4}
B. m∈[−5; 4]
C. m∈(−5; 4)\{−4}
D. m∈(−5; 4]\{−4}
Chọn D
Ta có limx→+∞y=1√2−1và limx→−∞y=−1√2+1 suy ra đồ thị hàm số có đường hai tiệm cận ngang là y=1√2−1và y=−1√2+1.
Để đồ thị có đúng bốn đường tiệm cận thì phương trình √2x2−2x−m−x−1=0 có hai nghiệm phân biệt khác 1
Ta có √2x2−2x−m−x−1=0⇔√2x2−2x−m=x+1 {x≥−1x2−4x−1=m (1)
Yêu cầu bài toán tương đương phương trình (1) có hai nghiệm phân biệt x≥−1 và x≠1.
Xét hàm số y=x2−4x−1 với x≥−1 và x≠1.
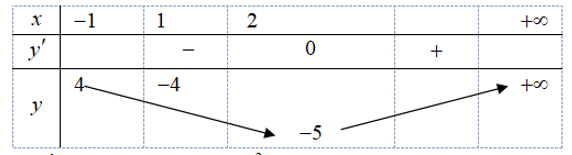
Bảng biến thiên:
Dựa vào bảng biến thiên phương trình x2−4x−1=m với x≥−1 và x≠1 có hai nghiệm thì m∈(−5; 4]\{−4}.