Cho tam giác nhọn ABC có ba đường cao AM, BN, CP cắt nhau tại H. Qua B kẻ tia Bx vuông góc với AB. Qua C kẻ tia Cy vuông góc với AC. Gọi D là giao điểm của Bx và Cy (Hình 15).

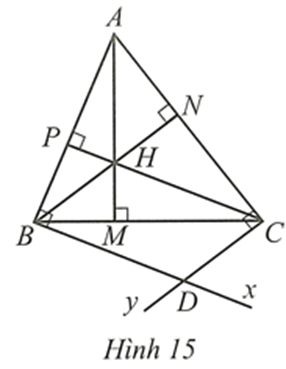
Tam giác ABC có điều kiện gì thì ba điểm A, D, H thẳng hàng?

Để ba điểm A, D, H thẳng hàng thì M phải thuộc DH.

Mà M thuộc BC, suy ra M là giao điểm của BC và DH.

Do BDCH là hình bình hành nên hai đường chéo BC và DH cắt nhau tại trung điểm mỗi đường. Suy ra M là trung điểm BC. Suy ra MB = MC

Xét ∆ABM và ∆ACM có:

MB = MC, \(\widehat {AMB} = \widehat {AMC} = 90^\circ \), cạnh AM chung

Do đó ∆ABM = ∆ACM (c.g.c). Suy ra AB = AC (hai cạnh tương ứng)

Dễ thấy, nếu tam giác ABC có AB = AC thì ba điểm A, D, H thẳng hàng.

Vậy tam giác ABC cân tại A thì ba điểm A, D, H thẳng hàng.