Cho hình bình hành ABCD có \(\widehat A > 90^\circ \), AB > BC. Trên đường thẳng vuông góc với BC tại C lấy hai điểm E, F sao cho CE = CF = BC. Trên đường thẳng vuông góc với CD tại C lấy hai điểm P, Q sao cho CP = CQ = CD (Hình 16). Chứng minh:
AC ⊥ EP.
Gọi H là giao điểm của AC và EP, K là giao điểm của AB và PQ.
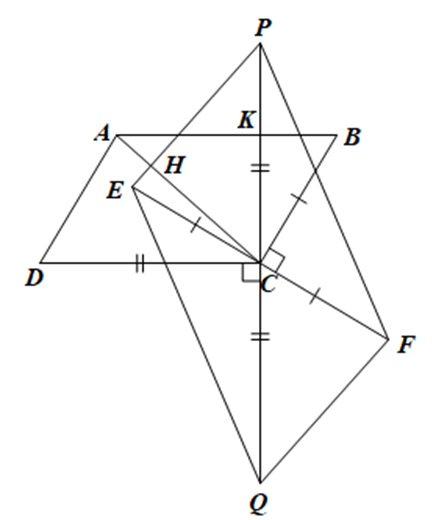
Do ABCD là hình bình hành nên AB // CD, AD = BC, \(\widehat B = \widehat D\).
Vì AB // CD nên \(\widehat {BKC} = \widehat {DCK} = 90^\circ \) (hai góc so le trong).
Suy ra tam giác BCK vuông tại K. Do đó \(\widehat B + \widehat {BCK} = 90^\circ \)
Mà \(\widehat B = \widehat D\), suy ra \(\widehat D + \widehat {BCK} = 90^\circ \).
Mặt khác, ta có \(\widehat {ECP} + \widehat {BCK} = \widehat {BCE} = 90^\circ \) nên \(\widehat D = \widehat {ECP}\).
Xét ∆ACD và ∆EPC có:
AD = EC (vì cùng bằng BC); \(\widehat D = \widehat {ECP}\); CD = PC.
Do đó ∆ACD = ∆EPC (c.g.c).
Suy ra \(\widehat {ACD} = \widehat {EPC}\) (hai góc tương ứng).
Mà \(\widehat {ACD} + \widehat {PCH} = \widehat {DCP} = 90^\circ \), suy ra \(\widehat {HPC} + \widehat {PCH} = 90^\circ \).
Xét tam giác CPH, ta có: \(\widehat {CHP} + \widehat {HPC} + \widehat {PCH} = 180^\circ \).
Suy ra \(\widehat {CHP} + 90^\circ = 180^\circ \) hay \(\widehat {CHP} = 90^\circ \).
Vậy \(AC \bot EP\).