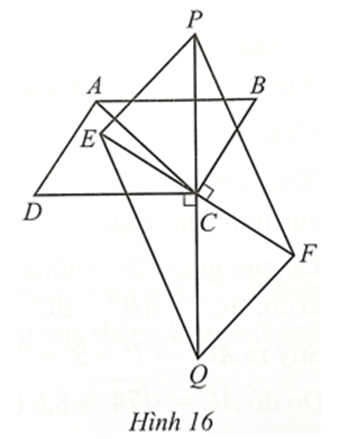
Cho hình bình hành ABCD có \(\widehat A > 90^\circ \), AB > BC. Trên đường thẳng vuông góc với BC tại C lấy hai điểm E, F sao cho CE = CF = BC. Trên đường thẳng vuông góc với CD tại C lấy hai điểm P, Q sao cho CP = CQ = CD (Hình 16). Chứng minh:

Tứ giác EPFQ là hình bình hành

Do CE = CF nên C là trung điểm của EF;

CP = CQ nên C là trung điểm PQ.

Tứ giác EPFQ có hai đường chéo EF và PQ cắt nhau tại trung điểm C của mỗi đường nên là hình bình hành.