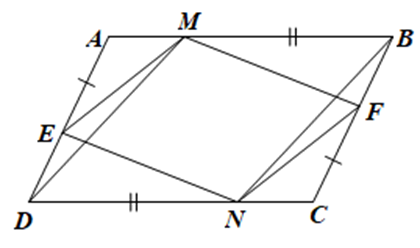
Cho hình bình hành ABCD. Trên cạnh AD, BC lần lượt lấy điểm E, F sao cho AE = CF. Trên cạnh AB, CD lần lượt lấy điểm M, N sao cho BM = DN. Chứng minh:

Tứ giác BMDN có BM = DN và BM // DN nên BMDN là hình bình hành.

Do ABCD, EMFN, BMDN đều là hình bình hành nên các đường chéo của mỗi hình bình hành cắt nhau tại trung điểm của mỗi đường.

Vậy AC, BD, EF, MN cùng đi qua trung điểm của mỗi đường.