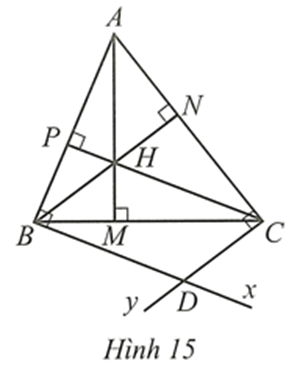
Cho tam giác nhọn ABC có ba đường cao AM, BN, CP cắt nhau tại H. Qua B kẻ tia Bx vuông góc với AB. Qua C kẻ tia Cy vuông góc với AC. Gọi D là giao điểm của Bx và Cy (Hình 15).

Do AM, BN, CP là đường cao của ∆ABC nên AM ⊥ BC, BN ⊥ AC, CP ⊥ AB

Do CP ⊥ AB, BD ⊥ AB nên CP // BD.

Do BN ⊥ AC, CD ⊥ AC nên BN // CD

Tứ giác BDCH có BD // CH, BH // CD nên BDCH là hình bình hành.