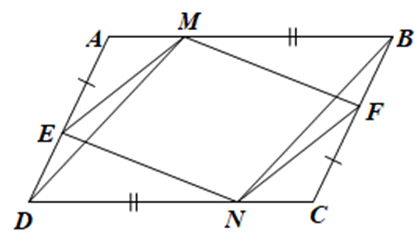
Cho hình bình hành ABCD. Trên cạnh AD, BC lần lượt lấy điểm E, F sao cho AE = CF. Trên cạnh AB, CD lần lượt lấy điểm M, N sao cho BM = DN. Chứng minh:
Tứ giác ENFM là hình bình hành;
Do ABCD là hình bình hành nên AD = BC và AB = CD; \(\widehat A = \widehat C\) và \(\widehat {ABC} = \widehat {CDA}\).
Mà AE = CF, AE + ED = AD, BF + CF = BC
Suy ra DE = BF.
Tương tự, ta cũng có AM = CN.
Xét ∆AEM và ∆CFN có:
AM = CN, \(\widehat A = \widehat C\), AE = CF
Do đó ∆AEM và ∆CFN (c.g.c). Suy ra EM = FN (hai cạnh tương ứng)
Xét ∆BFM và ∆DEN có:
BF = DE, \(\widehat {ABC} = \widehat {CDA}\), BM = DN
Do đó ∆BFM = ∆DEN (c.g.c). Suy ra FM = EN.
Tứ giác EMFN có EM = FN và FM = EN nên EMFN là hình bình hành.