Tam giác ABC có AB = 15 cm, AC = 20 cm, BC = 25 cm. Đường phân giác của góc BAC cắt BC tại D. Qua D vẽ DE // AB (E ∈ AC)

Bài 3 trang 57 Toán 8 Tập 2: Tam giác ABC có AB = 15 cm, AC = 20 cm, BC = 25 cm. Đường phân giác của góc BAC cắt BC tại D. Qua D vẽ DE // AB (E ∈ AC).

a) Tính độ dài các đoạn thẳng DB, DC và DE.

b) Chứng minh ABC là tam giác vuông. Tính diện tích tam giác ABC.

c) Tính diện tích các tam giác ADB, ADE và DCE.

Trả lời

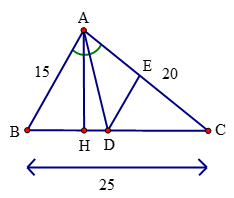
a) Trong tam giác ABC, ta có: AD là tia phân giác của $\widehat{BAC}$.

Suy ra: $\frac{DB}{DC}=\frac{AB}{AC}$(tính chất đường phân giác)

Mà AB = 15 cm; AC = 20 cm.

Nên $\frac{DB}{Dc}=\frac{15}{20}$

Suy ra: $\frac{DB}{DB+DC}=\frac{15}{15+20}$ (tính chất tỉ lệ thức)

Suy ra: $\frac{DB}{BC}=\frac{15}{35}$

Nên: $\mathrm{DB}=\frac{15}{35}.25=\frac{75}{7}\left(\mathrm{cm}\right)$

Do đó $DC=BC-BD=25-\frac{75}{7}=\frac{100}{7}\left(\mathrm{cm}\right)$

Xét tam giác ABC có DE // AB, theo hệ quả định lí Thalès, ta có:

$\frac{DE}{AB}=\frac{CD}{BC}\Rightarrow \frac{DE}{15}=\frac{{\displaystyle \frac{100}{7}}}{25}$

Vậy $\mathrm{DE}=\frac{60}{7}\mathrm{cm}$.

b) Xét tam giác ABC ta có: AB = 15 cm, AC = 20 cm, BC = 25 cm.

Nên ${\mathrm{BC}}^2=A{\mathrm{B}}^2+A{\mathrm{C}}^2$ suy ra tam giác ABC vuông tại A.

Khi đó, ta có: $S_{ABC}=\frac{1}{2}AC.AB=\frac{1}{2}.20.15=150\left(c{m}^2\right)$

Vậy diện tích tam giác ABC là 150 cm².

c) Kẻ AH ⊥ BC ta có: 

$\frac{S_{ADB}}{S_{ABC}}=\frac{{\displaystyle \frac{1}{2}}AH.BD}{{\displaystyle \frac{1}{2}}AH.BC}=\frac{DB}{DC}=\frac{{\displaystyle \frac{40}{7}}}{{\displaystyle \frac{30}{7}}}=\frac{4}{3}$

Suy ra $S_{ADB}=\frac{3}{7}\cdot S_{ABC}=\frac{3}{7}\cdot 150=\frac{450}{7}\left(c{m}^2\right)$

$\frac{S_{DCE}}{S_{ABC}}=\frac{\frac{1}{2}CE.DE}{\frac{1}{2}AC.AB}={\left(\frac{DE}{AB}\right)}^2={\left(\frac{\frac{60}{7}}{25}\right)}^2=\frac{144}{1225}$

Suy ra

$S_{DCE}=\frac{144}{1225}\cdot S_{ABC}=\frac{144}{1225}\cdot 150=\frac{864}{49}\left(c{m}^2\right)$

$S_{ADE}=S_{ABC}-S_{ADB}-S_{DCE}=150-\frac{450}{7}-\frac{864}{49}=\frac{3336}{49}\left(c{m}^2\right)$

Vậy $S_{ADB}=\frac{450}{7}c{m}^2; S_{DCE}=\frac{864}{49}c{m}^2; S_{ADE}=\frac{3336}{49}c{m}^2$

Xem thêm các bài giải SGK Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Định lí Thalès trong tam giác

Bài 2: Đường trung bình của tam giác

Bài 3: Tính chất đường phân giác của tam giác

Bài tập cuối chương 7

Bài 1: Hai tam giác đồng dạng

Bài 2: Các trường hợp đồng dạng của hai tam giác