Cho tam giác ABC vuông tại A có AB = 3 cm, AC = 4 cm. Đường phân giác của góc A cắt BC tại D

Bài 4 trang 57 Toán 8 Tập 2: Cho tam giác ABC vuông tại A có AB = 3 cm, AC = 4 cm. Đường phân giác của góc A cắt BC tại D.

a) Tính BC, DB, DC.

b) Vẽ đường cao AH. Tính AH, HD và AD.

Trả lời

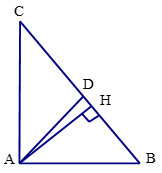
a) Tam giác ABC vuông tại A, áp dụng định lí Pythagore, ta có: 

$B{C}^2=A{C}^2+A{B}^2$ suy ra BC = 5 cm

AD là tia phân giác góc A nên $\frac{DB}{DC}=\frac{AB}{AC}$ suy ra $\frac{DB}{5-DB}=\frac{3}{4}$

$\Rightarrow 4DB=15-3DB\Rightarrow DB=\frac{15}{7}\left(cm\right).$

Do đó $DC=BC-DB=5-\frac{15}{7}=\frac{20}{7}\left(cm\right).$

Vậy BC = 5 cm, $DB=\frac{15}{7}\mathrm{cm}$, $DC=\frac{20}{7}\mathrm{cm}$

b) Ta có: $S_{ABC}=\frac{1}{2}AB.AC=\frac{1}{2}AH.BC$

$\Rightarrow A\mathrm{H}=\frac{AB.AC}{BC}=\frac{3.4}{5}=\frac{12}{5}\left(\mathrm{cm}\right)$

Tam giác ABH vuông tại H nên 

$HB=\sqrt{A{B}^2-A{H}^2}=\sqrt{3^2-{\left(\frac{12}{5}\right)}^2}=\frac{9}{5}\left(\mathrm{cm}\right)$

Ta có: $HD=DB-HB=\frac{15}{7}-\frac{9}{5}=\frac{12}{35}$(cm)

Tam giác ABH vuông tại H nên 

$AD=\sqrt{H{D}^2+A{H}^2}=\sqrt{{\left(\frac{12}{35}\right)}^2+{\left(\frac{12}{5}\right)}^2}=\frac{12\sqrt{2}}{7}\left(cm\right)$

Vậy $A\mathrm{H}=\frac{12}{5}\mathrm{cm}$, $\mathrm{HD}=\frac{12}{35}\mathrm{cm}$, $AD=\frac{12\sqrt{2}}{7}\mathrm{cm}$.

Xem thêm các bài giải SGK Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Định lí Thalès trong tam giác

Bài 2: Đường trung bình của tam giác

Bài 3: Tính chất đường phân giác của tam giác

Bài tập cuối chương 7

Bài 1: Hai tam giác đồng dạng

Bài 2: Các trường hợp đồng dạng của hai tam giác