Ở hình bên, độ dài các cạnh AB, BC và GH đã được cho theo a và b; hai cạnh CD và EF bằng nhau; ba cạnh AH, GF và ED bằng nhau

Bài 16 trang 27 SBT Toán 8 Tập 1: Ở hình bên, độ dài các cạnh AB, BC và GH đã được cho theo a và b; hai cạnh CD và EF bằng nhau; ba cạnh AH, GF và ED bằng nhau.

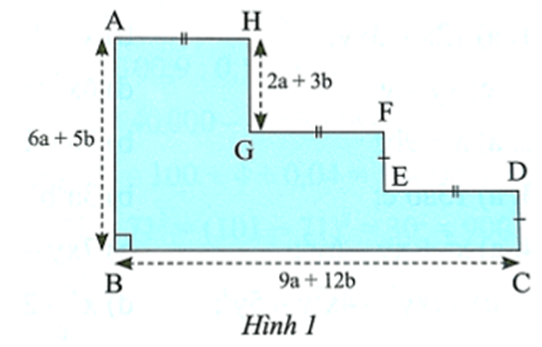
a) Tìm độ dài các cạnh AH, GF, ED.

b) Tìm độ dài các cạnh CD, EF.

c) Tính chu vi của hình bên.

Trả lời

a) Ta có: AH = GF = ED và AH + GF + ED = BC

Nên $AH=GF=ED=\frac{BC}{3}=\frac{9a+12b}{3}=\frac{3(3a+4b)}{3}=3a+4b$.

b) Ta có:

EF + CD = AB ‒ GH

= 6a + 5b ‒ (2a + 3b) = 6a + 5b ‒ 2a ‒ 3b = 4a + 2b.

Mà EF = CD nên $EF=CD=\frac{4a+2b}{2}=\frac{2(2a+b)}{2}=2a+b$.

c) Chu vi hình vẽ là:

AB + BC + CD + DE + EF + FG + GH + HA

= AB + BC + (CD + EF + GH) + (DE + FG + HA)

= AB + BC + AB + BC

= 2AB + 2BC

= 2(6a + 5b) + 2(9a + 12b)

= 12a + 10b + 18a + 24b

= 30a + 34b.

Xem thêm các bài giải sách bài tập Toán 8 Chân trời sáng tạo hay, chi tiết khác:

Bài 6: Cộng, trừ phân thức

Bài 7: Nhân, chia phân thức

Bài tập cuối chương 1 trang 26

Bài 1: Hình chóp tam giác đều

Bài 2: Diện tích xung quanh và thể tích của hình chóp tam giác đều, hình chóp tứ giác đều

Bài tập cuối chương 2 trang 44