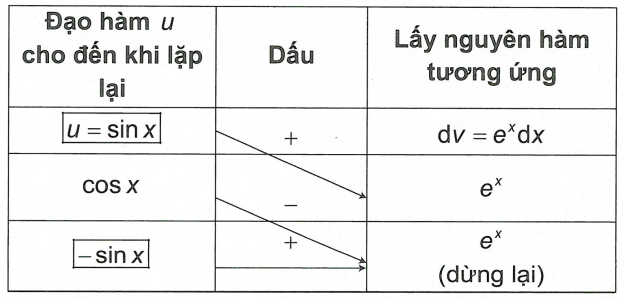
Nguyên hàm I = e^xsin xdx là: A. 2e^x( sin x + cos x) + C B. 2e^x( sin x - cos x) + C C. 1/2e^x( sin x - cos x) + C D. 1/2e^x( sin x + cos x) + C
Nguyên hàm \[I = \int {{e^x}\sin xdx} \] là:
A. \[2{e^x}\left( {\sin x + \cos x} \right) + C\]
B. \[2{e^x}\left( {\sin x - \cos x} \right) + C\]
C. \[\frac{1}{2}{e^x}\left( {\sin x - \cos x} \right) + C\]
D. \[\frac{1}{2}{e^x}\left( {\sin x + \cos x} \right) + C\]