Một thiết bị tiệt khuẩn y tế bằng năng lượng mặt trời được mua với giá 60 triệu đồng

Bài 26 trang 62 SBT Toán 8 Tập 1: Một thiết bị tiệt khuẩn y tế bằng năng lượng mặt trời được mua với giá 60 triệu đồng, mỗi năm thiết bị tiệt khuẩn đó đều khấu hao $k$ (triệu đồng) với $0<k<60$. Gọi $y$ (triệu đồng) là giá của thiết bị tiệt khuẩn đó sau $x$ năm sử dụng.

a) Chứng tỏ rẳng $y$ là hàm số bậc nhất của $x$, tức là $y=ax+b\left(a\ne 0\right)$.

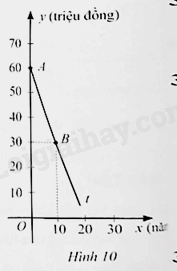
b) Trong Hình 10, tia $At$ là một phần của đường thẳng $y=ax+b$. Tìm $a,b$. Từ đó, cho biết sau 12 năm sử dụng thì giá của thiết bị tiệt khuẩn đó bằng bao nhiêu phần trăm so với giá mua ban đầu.

Trả lời

a) Công thức biểu thị giá của thiết bị tiệt khuẩn đó sau $x$ năm sử dụng là: $y=60-kx$ hay $y=-kx+60$. Mà $k\ne 0$, suy ra $y$ là hàm số bậc nhất của $x$.

b) Từ câu a, ta có $b=60$. Do đường thẳng $y=ax+b$ đi qua điểm $B\left(10;30\right)$ nên $30=a.10+60$. Suy ra $a=-3$. Khi đó, đường thẳng cần tìm là: $y=-3x+60$.

Giá của thiết bị tiệt khuẩn đó sau 12 năm sử dụng là:

$-3.12+60=24$ (triệu đồng)

Tỉ số phần trăm giữa giá của thiết bị tiệt khuẩn đó sau 12 năm sử dụng và giá mua ban đầu là: $\frac{24.100}{60}\mathrm{\%}=40\mathrm{\%}$.

Vậy sau 12 năm sử dụng thì giá của thiết bị tiệt khuẩn đó bằng $40\mathrm{\%}$ so với giá mua ban đầu.

Xem thêm các bài giải SBT Toán 8 Cánh diều hay, chi tiết khác:

Bài 2: Mặt phẳng tọa độ. Đồ thị của hàm số

Bài 3: Hàm số bậc nhất y = ax + b (a ≠ 0)

Bài 4: Đồ thị hàm số bậc nhất y = ax + b (a ≠ 0)

Bài tập cuối chương 3

Bài 1: Hình chóp tam giác đều

Bài 2: Hình chóp tứ giác đều