Một chiếc thuyền xuất phát từ vị trí I chở hàng cho hai hòn đảo A và B theo phương thẳng (được minh họa như trong hình vẽ). Một người đứng ở vị trí K trên bờ quan sát ba điểm thẳng hàng I, A,
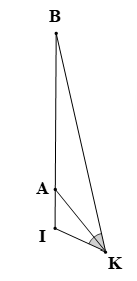
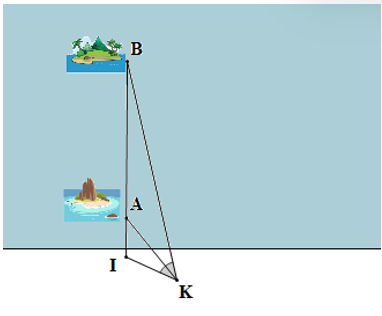
Một chiếc thuyền xuất phát từ vị trí I chở hàng cho hai hòn đảo A và B theo phương thẳng (được minh họa như trong hình vẽ). Một người đứng ở vị trí K trên bờ quan sát ba điểm thẳng hàng I, A, B. Người đó nhận thấy góc nhìn đến hai điểm I, A thì bằng góc nhìn đến hai điểm A, B, tức là Biết rằng thuyền đi từ vị trí I đến hòn đảo A là 500 m; từ hòn đảo A đến hòn đảo B là 6 km và khoảng cách từ người đó đến vị trí I là 1 km. Tính khoảng cách từ người đó (vị trí K) đến hòn đảo B?

A. 10 km;
B. 20 km;
C. 15 km;
D. 12 km.