Gọi M, N, P là các điểm trên đường tròn lượng giác sao cho số đo của các góc lượng giác
6.4k
25/07/2023
Bài 1 trang 15 Toán 11 Tập 1: Gọi M, N, P là các điểm trên đường tròn lượng giác sao cho số đo của các góc lượng giác lần lượt bằng . Chứng minh rằng tam giác MNP là tam giác đều.
Phương pháp giải:
Dựa vào các giá trị lượng giác để tính từng cạnh của tam giác MNP
Trả lời
Hình minh họa:
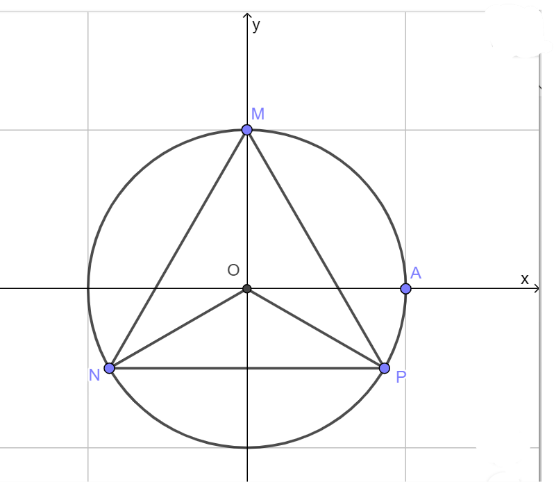
Cung MP = cung NP = cung NM
đều
Cung MP = cung NP = cung NM
đều
Xem thêm lời giải bài tập Toán lớp 11 Cánh diều hay, chi tiết khác:
Bài 1: Góc lượng giác. Giá trị lượng giác của góc lượng giác
Bài 2: Các phép biến đổi lượng giác
Bài 3: Hàm số lượng giác và đồ thị
Bài 4: Phương trình lượng giác cơ bản
Bài tập cuối chương 1
Bài 1: Dãy số

