Gọi ( H ) là hình phẳng giới hạn bởi đồ thị hàm số y = e^x, trục hoành và các đường thẳng x = - 1, x = 1. Với k ( - 1;1), đường thẳng x = k chia hình phẳng ( H ) thành hai hình phẳng có diệ
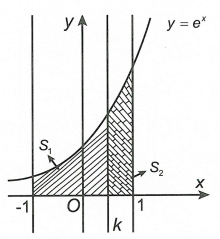
Gọi \(\left( H \right)\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = {e^x}\), trục hoành và các đường thẳng \(x = - 1\), \(x = 1\). Với \(k \in \left( { - 1;1} \right)\), đường thẳng \(x = k\) chia hình phẳng \(\left( H \right)\) thành hai hình phẳng có diện tích lần lượt là \({S_1}\) và \({S_2}\) (như hình vẽ bên). Giá trị k để \({S_1} = {S_2}\) là
A. \(2\ln 2 - 1\).
B. \(2\ln \left( {e - \frac{1}{e}} \right) - 1\).
C. \(\ln \left( {e + \frac{1}{e}} \right) - \ln 2\).
D. \(\ln 2\).
