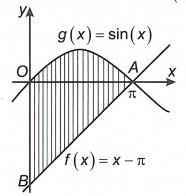
Cho hình phẳng ( H ) giới hạn bởi các đường ( C1 ): f( x ) = x - pi, ( C2 ): g( x ) = sin x và x = 0. Gọi V là thể tích khối tròn xoay tạo thành do ( H ) quay quanh trục hoành và V = p pi ^2,
8
19/04/2024
Cho hình phẳng \(\left( H \right)\) giới hạn bởi các đường \(\left( {{C_1}} \right)\): \(f\left( x \right) = x - \pi \), \(\left( {{C_2}} \right)\): \(g\left( x \right) = \sin x\) và \(x = 0\). Gọi V là thể tích khối tròn xoay tạo thành do \(\left( H \right)\) quay quanh trục hoành và \(V = p{\pi ^2}\), \(p \in \left( \mathbb{Q} \right)\). Giá trị của 24p bằng
A. 8.
B. 4.
C. 24.
D. 12.
Trả lời
Hướng dẫn giải
Xét phương trình hoành độ giao điểm của đồ thị các hàm số \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right)\) là
\(x - \pi = \sin x \Leftrightarrow x - \pi - \sin x = 0\) \(\left( 1 \right)\).
Xét hàm số \(h\left( x \right) = x - \pi - \sin x \Rightarrow h'\left( x \right) = 1 - \cos x \ge 0\), \(\forall x \in \mathbb{R}\).
Suy ra \(h\left( x \right)\) đồng biến trên \(\mathbb{R}\) và \(x = \pi \) là một nghiệm của phương trình \(\left( 1 \right)\) nên \(x = \pi \) là nghiệm duy nhất của phương trình \(\left( 1 \right)\).
Do đó thể tích khối tròn xoay tạo thành khi quay \(\left( H \right)\) quanh trục hoành là thể tích của khối nón khỉ quay tam giác vuông OAB quanh trục hoành.
\(V = \frac{1}{3}.\pi .O{B^2}.OA = \frac{1}{3}.\pi .{\pi ^2}.\pi = \frac{1}{3}{\pi ^4} \Rightarrow p = \frac{1}{3}\)
Vậy \(24p = 24.\frac{1}{3} = 8\).
Chọn A.
