Để chuẩn bị cho đêm hội diễn văn nghệ chào đón năm mới, bạn An đã làm một chiếc mũ “cách điệu” cho ông già Noel có dáng một khối tròn xoay. Mặt cắt qua trục của chiếc mũ như hình vẽ bên. Biết
52
19/04/2024
Để chuẩn bị cho đêm hội diễn văn nghệ chào đón năm mới, bạn An đã làm một chiếc mũ “cách điệu” cho ông già Noel có dáng một khối tròn xoay. Mặt cắt qua trục của chiếc mũ như hình vẽ bên. Biết rằng \(OO' = 5\,cm\), \(OA = 10\,cm\), \(OB = 20\,cm\), đường cong AB là một phần của parabol có đỉnh là điểm A. Thể tích của chiếc mũ bằng
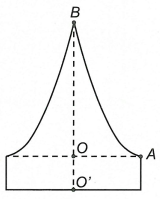
A. \(\frac{{2750\pi }}{3}c{m^3}\).
B. \(\frac{{2500\pi }}{3}c{m^3}\).
C. \(\frac{{2050\pi }}{3}c{m^3}\).
D. \(\frac{{2250\pi }}{3}c{m^3}\).
Trả lời
Hướng dẫn giải
Ta gọi:
+) Thể tích của chiếc mũ là V.
+) Thể tích của khối trụ có bán kính đáy bằng \(OA = 10\,cm\)cm và đường cao \(OO' = 5\,cm\)là \({V_1}\).
+) Thể tích của vật thể tròn xoay khi quay hình phẳng giới hạn bởi đường cong AB và hai trục tọa độ quanh trục Oy là \({V_2}\).
Khi đó \({V_1} = {5.10^2}\pi = 500\pi \) và \(V = {V_1} + {V_2}\).
Chọn hệ trục tọa độ như hình vẽ.
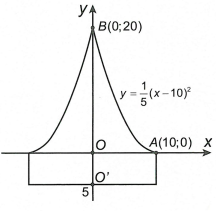
Do parabol có đỉnh A nên nó có phương trình dạng \(\left( P \right)\): \(y = a{\left( {x - 10} \right)^2}\).
Vì \(\left( P \right)\) qua điểm \(B\left( {0;20} \right)\) nên \(a = \frac{1}{5}\).
Do đó \(\left( P \right)\): \(y = \frac{1}{5}{\left( {x - 10} \right)^2}\). Từ đó suy ra \(x = 10 - \sqrt {5y} \)(do \(x < 10\) ).
Suy ra \({V_2} = \pi \int\limits_0^{20} {{{\left( {10 - \sqrt {5y} } \right)}^2}dy} = \pi \left( {3000 - \frac{{8000}}{3}} \right) = \frac{{1000}}{3}\pi \left( {c{m^3}} \right)\).
Vậy \(V = {V_1} + {V_2} = \frac{{1000}}{3}\pi + 500\pi = \frac{{2500}}{3}\pi \left( {c{m^3}} \right)\)
Chọn B.


