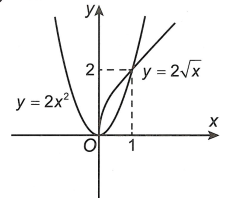
Cho hình phẳng ( H ) giới hạn bởi hai đồ thị ( C1): y = 2x^2 và ( C2): y^2 = 4x. Quay hình phẳng ( H ) xung quanh trục Ox ta thu được khối tròn xoay có thể tích là A. V = 88pi /5 B. V = 9p
11
19/04/2024
Cho hình phẳng \(\left( H \right)\) giới hạn bởi hai đồ thị \(\left( {{C_1}} \right)\): \(y = 2{x^2}\) và \(\left( {{C_2}} \right)\): \({y^2} = 4x\). Quay hình phẳng \(\left( H \right)\) xung quanh trục Ox ta thu được khối tròn xoay có thể tích là
A. \(V = \frac{{88\pi }}{5}\).
B. \(V = \frac{{9\pi }}{{70}}\).
C. \(V = \frac{{4\pi }}{3}\).
D. \(V = \frac{{6\pi }}{5}\).
Trả lời
Hướng dẫn giải
Tọa độ giao điểm của \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right)\) là nghiệm của hệ phương trình
\(\left\{ \begin{array}{l}y = 2{x^2}\\{y^2} = 4x\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = y = 0\\x = 1;y = 2\end{array} \right.\)
Với \(x \in \left[ {0;1} \right]\) thì \({y^2} = 4x \Leftrightarrow y = 2\sqrt x \) .
Vậy thể tích của khối tròn xoay cần tính là \(V = \pi \int\limits_0^1 {\left| {{{\left( {2{x^2}} \right)}^2} - {{\left( {2\sqrt x } \right)}^2}} \right|dx} \)
\( = \pi \int\limits_0^1 {\left( {4x - 4{x^2}} \right)dx} = \frac{{6\pi }}{5}\)
Chọn A.
