Có 2 vật M và N thoạt đầu cách nhau khoảng l. Cùng lúc 2 vật chuyển động thẳng đều, m chạy về B với vận tốc v1, N chạy về C với vận tốc v2. Tính khoảng cách ngắn nhất giữa hai vật và thời gian để đạt khoảng cách ngắn nhất giữa hai vật kể từ lúc bắt đầu chuyển động.
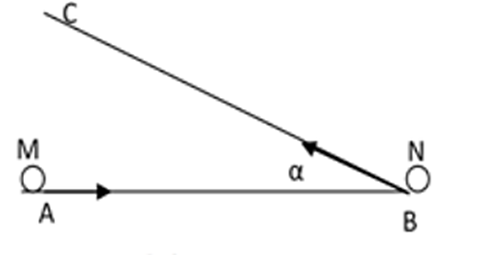
Sau khoảng thời gian t:
dM/B = l – v1 . t
dB/N = V2 . t
Áp dụng công thức hàm số côsin
\[{d_{MN}} = \sqrt {{{(l - {v_1}t)}^2} + {{({v_2}t)}^2} - 2.(l - {v_1}t){v_2}t.\cos \alpha } \]
\[ \Rightarrow {d^2} = {l^2} - 2{v_1}.l.t + {v_1}^2.{t^2} + {v_2}^2.{t^2} + 2.{v_1}.{v_2}.{t^2}.\cos \alpha - 2l.{v_2}.t.\cos \alpha \]
\[ \Rightarrow {d^2} = ({v_1}^2 + {v_2}^2 + 2.{v_1}{v_2}\cos \alpha ){t^2} - 2l({v_1} - {v_2}\cos \alpha ).t + {l^2}(1)\]
Nhận xét (l) là một hàm số bậc hai của t.
Do đó: \[{d_{\min }} = \sqrt {\frac{{ - \Delta }}{{4a}}} \]
\[ = \sqrt {\frac{{ = \sqrt {4\left[ {({v_1}^2 + {v_2}^2 + 2.{v_1}{v_2}\cos \alpha ){l^2}} \right]} - 4{l^2}{{({v_1} - {v_2}\cos \alpha )}^2}}}{{\sqrt {({v_1}^2 + {v_2}^2 + 2.{v_1}{v_2}\cos \alpha )} }}} \]
\[ = \frac{{l{v_2}\sin \alpha }}{{{v_1}^2 + {v_2}^2 + 2.{v_1}{v_2}\cos \alpha }}\].
Khi đó \[{t_{\min }} = \frac{{2l({v_1} - {v_2}\cos \alpha )}}{{2({v_1}^2 + {v_2}^2 + 2.{v_1}{v_2}\cos \alpha )}}\]
Vậy \[{d_{\min }} = \frac{{l{v_2}\sin \alpha }}{{{v_1}^2 + {v_2}^2 + 2.{v_1}{v_2}\cos \alpha }}\]; \[{t_{\min }} = \frac{{2l({v_1} - {v_2}\cos \alpha )}}{{2({v_1}^2 + {v_2}^2 + 2.{v_1}{v_2}\cos \alpha )}}\].