1900.edu.vn - Tin tức mới nhất - Cập nhật hàng ngày
1900.edu.vn - Tin tức mới nhất - Cập nhật hàng ngày
Hỏi đáp

Cho tam giác ABC = tam giác MNP. Tia phân giác của góc BAC và NMP lần lượt cắt các cạnh BC và NP tại D, Q

557 16/11/2023

Bài 6 trang 92 Toán 7 Tập 2: Cho ∆ABC = ∆MNP. Tia phân giác của góc BAC và NMP lần lượt cắt các cạnh BC và NP tại D, Q. Chứng minh AD = MQ.

Trả lời

GT

∆ABC = ∆MNP,

AD là tia phân giác của BAC^, 

MQ là tia phân giác của NMP^, 

KL

AD = MQ.

Chứng minh (Hình vẽ dưới đây):

 

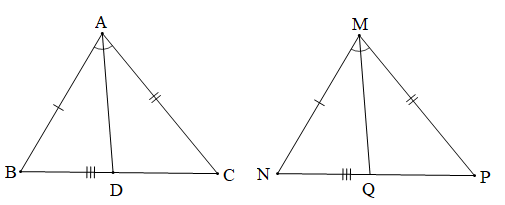
Giải Toán 7 Bài 6 (Cánh diều): Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc (ảnh 1) 

Vì ∆ABC = ∆MNP (giả thiết) nên:

+) BAC^=NMP^ và B^=N^ (các cặp góc tương ứng);

+) AB = MN (hai cạnh tương ứng).

Ta có:

+) AD là tia phân giác của BAC^ (giả thiết) nên BAD^=12BAC^ (tính chất tia phân giác của một góc)

+) MQ là tia phân giác của NMP^ (giả thiết) nên NMQ^=12NMP^ (tính chất tia phân giác của một góc)

Mà BAC^=NMP^ (chứng minh trên) nên BAD^=NMQ^.

Xét ∆ABD và ∆MNQ có:

BAD^=NMQ^ (chứng minh trên),

AB = MN (chứng minh trên),

B^=N^ (chứng minh trên).

Suy ra ∆ABD = ∆MNQ (g.c.g).

Do đó AD = MQ (hai cạnh tương ứng).

Vậy AD = MQ.

Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:

Bài 4: Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh

Bài 5: Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh

Bài 6: Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc

Bài 7: Tam giác cân

Bài 8: Đường vuông góc và đường xiên

Bài 9: Đường trung trực của một đoạn thẳng

Câu hỏi cùng chủ đề

Cho tam giác ABC có góc B > góc C. Tia phân giác góc BAC cắt cạnh BC tại điểm D. Chứng minh góc ADB < góc ADC

Bài 5 trang 92 Toán 7 Tập 2. Cho tam giác ABC có B^>C^. Tia phân giác góc BAC cắt cạnh BC tại điểm D. a) Chứng minh ADB^

Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc
1.6k 1 năm trước

Cho Hình 67 có góc AHD = góc BKC = 90°, DH = CK, góc DAB = góc CBA. Chứng minh AD = BC

Bài 4 trang 92 Toán 7 Tập 2. Cho Hình 67 có AHD^=BKC^=90°, DH = CK, DAB^=CBA^. Chứng minh AD = BC.

Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc
635 1 năm trước

Cho Hình 66 có góc N = góc P = 90°, góc PMQ = góc NQM. Chứng minh MN = QP, MP = QN

Bài 3 trang 92 Toán 7 Tập 2. Cho Hình 66 có N^=P^=90°,PMQ^=NQM^. Chứng minh MN = QP, MP = QN.

Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc
413 1 năm trước

Cho Hình 65 có AM = BN, góc A = góc B. Chứng minh: OA = OB, OM = ON

Bài 2 trang 91 Toán 7 Tập 2. Cho Hình 65 có AM = BN, A^=B^. Chứng minh. OA = OB, OM = ON.

Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc
277 1 năm trước

Cho hai tam giác ABC và A'B'C' thỏa mãn: AB = A'B', góc A = góc A', góc C = góc C'. Hai tam giác ABC và A'B'C' có bằng nhau không? Vì sao

Bài 1 trang 91 Toán 7 Tập 2. Cho hai tam giác ABC và A'B'C' thỏa mãn. AB = A'B', A^=A'^, C^=C'^. Hai tam giác ABC và A'B'C' có bằng nhau không? Vì sao?

Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc
522 1 năm trước

Giải thích bài toán ở phần mở đầu

Luyện tập 2 trang 89 Toán 7 Tập 2. Giải thích bài toán ở phần mở đầu.

Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc
201 1 năm trước

Cho hai tam giác ABC và A'B'C' thỏa mãn: BC = B'C' = 3 cm, góc B = góc B' = 60°, góc C = 50°, góc A' = 70. Hai tam giác ABC và A'B'C' có bằng nhau không?

Luyện tập 1 trang 89 Toán 7 Tập 2. Cho hai tam giác ABC và A'B'C' thỏa mãn. BC = B'C' = 3 cm, B^=B'^=60°, C^=50°, A'^=70°. Hai tam giác ABC và A'B'C' có bằng nhau không? Vì sao?

Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc
431 1 năm trước

Cho hai tam giác ABC và A'B'C' (Hình 57) có: góc A = góc A', AB = A'B' = 3 cm, góc B = góc B' = 45°

Hoạt động 2 trang 88 Toán 7 Tập 2. Cho hai tam giác ABC và A'B'C' (Hình 57) có. A^=A'^=60°, AB = A'B' = 3 cm, B^=B'^=45°. Bằng cách đếm số ô vuông, hãy so sánh BC và B'C'. Từ đó có thể kết luận được hai tam giác ABC và A'B'C' bằng nhau hay không?

Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc
306 1 năm trước

Cho tam giác ABC. Những góc nào của tam giác ABC có cạnh thuộc đường thẳng AB

Hoạt động 1 trang 88 Toán 7 Tập 2. Cho tam giác ABC (Hình 56). Những góc nào của tam giác ABC có cạnh thuộc đường thẳng AB? Trong tam giác ABC (Hình 56), ta gọi góc A và góc B là hai góc kề cạnh AB. Tương tự, góc B và góc C là hai góc kề cạnh BC, góc C và góc A là hai góc kề cạnh CA.

Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc
191 1 năm trước

Có ba trạm quan sát A, B, C trong đó trạm quan sát C ở giữa hồ

Câu hỏi khởi động trang 88 Toán 7 Tập 2. Có ba trạm quan sát A, B, C trong đó trạm quan sát C ở giữa hồ. Người ta muốn đo khoảng cách từ A và từ B đến C. Do không thể đo trực tiếp được các khoảng cách trên nên người ta làm như sau (Hình 55). - Đo góc BAC được 60°, đo góc ABC được 45°; - Kẻ tia Ax sao cho BAx^=60°, kẻ tia By sao cho ABy^=45°, xác định giao điểm D của hai tia đó; - Đo khoảng cách AD...

Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc
189 1 năm trước
Xem tất cả

Danh mục