Cho tứ giác ABCD như Hình 12. Tính độ dài hai đường chéo và cạnh còn lại của tứ giác ABCD

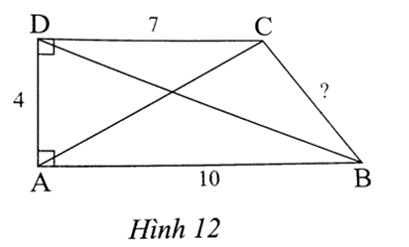
Bài 3 trang 57 SBT Toán 8 Tập 1: Cho tứ giác ABCD như Hình 12.

a) Tính độ dài hai đường chéo và cạnh còn lại của tứ giác ABCD.

b) Cho biết góc B bằng 53°. Tìm số đo góc C.

Trả lời

a) Áp dụng định lý Pythagore trong tam giác ABD vuông tại A có:

BD² = AD² + AB² = 4² + 10² = 116

Suy ra $BD=\sqrt{116}$.

Áp dụng định lý Pythagore trong tam giác ADC vuông tại D có:

AC² = AD² + DC² = 4² + 7² = 65

Suy ra $AC=\sqrt{65}$.

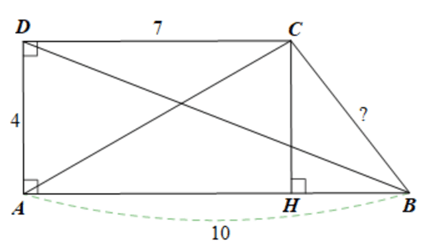
Kẻ CH ⊥ AB (H ∈ AB), mà AD ⊥ AB nên CH // AD

Ta cũng có DC ⊥AD và AB ⊥ AD nên DC // AB

Suy ra $\widehat{DCA}=\widehat{HAC},\widehat{DAC}=\widehat{HCA}$ (các cặp góc so le trong)

Xét ∆ADC và ∆CHA có:

$\widehat{DCA}=\widehat{HAC}$ cạnh AC chung, $\widehat{DAC}=\widehat{HCA}$

Do đó ∆ADC = ∆CHA (g.c.g)

Suy ra: CD = AH, AD = CH

Mà CD = 7, AD = 4 nên AH = 7, CH = 4

Ta có: BH = AB ‒ AH = 10 ‒ 7 =3.

Áp dụng định lý Pythagore trong tam giác CBH vuông tại H có:

BC² = CH² + BH² = 3² + 4² = 25

Suy ra $BC=\sqrt{25}=5$.

b) Vì tổng số đo các góc của một tứ giác bằng 360° nên trong tứ giác ABCD có:

$\hat{A}+\hat{B}+\hat{C}+\hat{D}=360°$

Suy ra $\hat{C}=360°-\hat{A}-\hat{B}-\hat{D}$$=360°-90°-53°-90°=127°$.

Xem thêm các bài giải sách bài tập Toán 8 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 2 trang 44

Bài 1: Định lí Pythagore

Bài 2: Tứ giác

Bài 3: Hình thang – Hình thang cân

Bài 4: Hình bình hành – Hình thoi

Bài 5: Hình chữ nhật – Hình vuông