Giải SBT Toán 8 Bài 3: Hình thang – Hình thang cân
Lời giải:
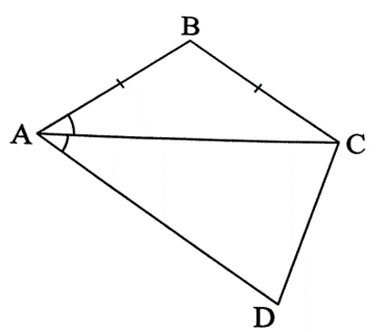
Ta có AB = BC nên ∆ABC cân tại B, suy ra .
Mặt khác, (do AC là tia phân giác của ).
Suy ra , mà 2 góc này ở vị trí so le trong
Do đó BC // AD.
Vậy tứ giác ABCD là hình thang.
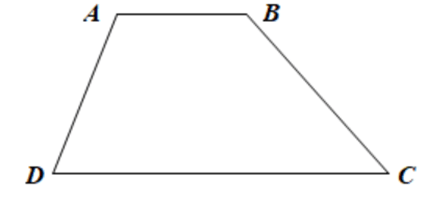
Bài 2 trang 60 SBT Toán 8 Tập 1: Tứ giác ABCD có . Chứng minh tứ giác ABCD là hình thang.
Lời giải:
Tứ giác ABCD có tổng 4 góc bằng 360° nên .
Mà
Do đó hay .
Suy ra AB // CD.
Vậy tứ giác ABCD là hình thang.
Lời giải:
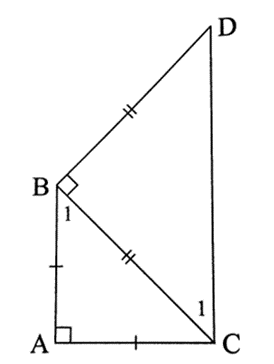
Ta có ∆ABC vuông cân tại A, ∆BCD vuông cân tạiB suy ra .
Vì và là hai góc ở vị trí so le trong nên AB // CD.
Vậy tứ giác ABDC là hình thang.
Hình thang ABDC có nên ABDC là hình thang vuông.
Lời giải:
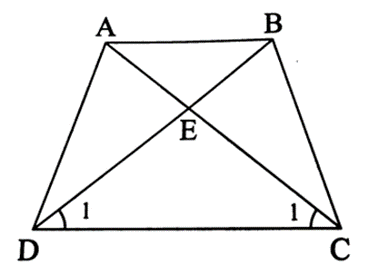
Gọi E là giao điểm của AC và BD.
Trong ∆ECD, ta có nên ∆ECD cân tại E, suy ra EC = ED.(1)
Ta có: AB // CD nên
⦁ (hai góc so le trong);
⦁ (hai góc so le trong);
⦁ (giả thiết).
Suy ra , do đó ∆BEA cân tại E.
Nên AE = BE. (2)
Ta có: AC = AE + EC; BD = BE + ED (3)
Từ (1), (2) và (3) suy ra AC = BD.
Hình thang ABCD có hai đường chéo bằng nhau nên ABCD là hình thang cân.
Lời giải:
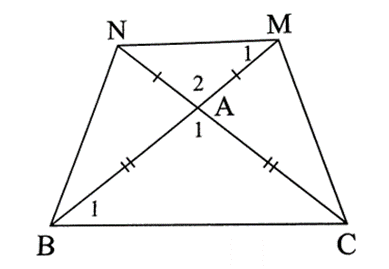
Xét ∆AMN có AM = AN (giả thiết).
Do đó ∆AMN cân tại A, suy ra .
Vì ∆ABC cân tại A nên .
Lại có (hai góc đối đỉnh) nên .
Mà hai góc này ở vị trí so le trong nên MN // BC.
Vậy tứ giác MNBC là hình thang.(1)
Mặt khác, AB = AC; AM = AN.
Suy ra AB + AM = AC + AN, do đó MB = NC (2)
Từ (1) và (2) suy ra MNBC là hình thang cân.
Lời giải:
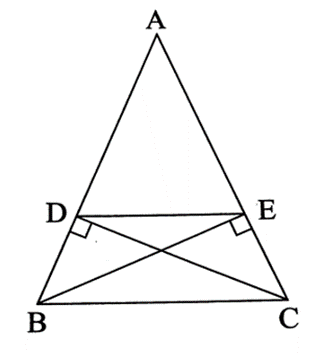
Do BE, CD là hai đường cao nên BE ⊥ AC, CD ⊥ AB.
Xét ∆BEC vuông tại E và ∆CDB vuông tại D, ta có:
BC là cạnh chung; (do ∆ABC cân tại A)
Do đó ∆BEC = ∆CDB (cạnh huyền – góc nhọn)
Suy ra EC = BD (hai cạnh tương ứng)
Mà AC = AB nên AC ‒ EC = AB ‒ BD, hay AE = AD
Do đó ∆ADE cân tại A suy ra . (1)
Vì ∆ABC cân tại A nên . (2)
Từ (1) và (2) suy ra .
Mà hai góc này ở vị trí đồng vị nên DE // BC
Suy ra tứ giác BDEC là hình thang.
Hìnhthang BDEC có nên là hình thang cân.
Xem thêm lời giải Sách bài tập Toán 8 bộ sách Chân trời sáng tạo hay, chi tiết khác:
Bài 4: Hình bình hành – Hình thoi
Bài 5: Hình chữ nhật – Hình vuông
Bài tập cuối chương 3 trang 72
