Giải SBT Toán 8 (Chân trời sáng tạo) Bài 1: Định lí Pythagore

Giải SBT Toán 8 Bài 1: Định lí Pythagore

Bài 1 trang 52 SBT Toán 8 Tập 1: Cho tam giác MNP vuông tại M.

a) Tính độ dài cạnh NP nếu biết MN = 7, MP = 24.

b) Tính độ dài cạnh MP nếu biết NP = 29, MN = 20.

c) Tính độ dài cạnh MN nếu biết NP = 61, MP = 11.

Lời giải:

a) Áp dụng định lý Pythagore vào tam giác MNP vuông tại M, ta có:

NP² = MN² + MP² = 7² + 24² = 49 + 576 = 625.

Suy ra $NP=\sqrt{625}=25$.

b) Từ NP² = MN² + MP², suy ra MP² = NP² ‒ MN² = 29² ‒ 20² = 441.

Suy ra $MP=\sqrt{441}=21$.

c) Từ NP² = MN² + MP², suy ra MN² = NP² ‒ MP² = 61² ‒ 11² = 3600.

Suy ra $MN=\sqrt{3600}=60$.

Bài 2 trang 52 SBT Toán 8 Tập 1: Chứng minh tam giác EFG vuông trong các trường hợp sau:

a) FG = 12, EF = 35, EG = 37;

b) FG = 85, EF = 77, EG = 36;

c) FG = 12, EF = 13, EG = 5.

Lời giải:

a) Ta có EG² = 37² = 1 369 và EF² + FG² = 35² + 12² = 1 369.

Suy ra tam giác EFG vuông tại F (định lí Pythagore đảo).

b) Ta có FG² = 85² = 7 225 và EF² + EG² = 77² + 36² =7 225.

Suy ra tam giác EFG vuông tại E (định lí Pythagore đảo).

c) Ta có EF² = 13² = 169 và EG² + FG² = 12² + 5² = 169.

Suy ra tam giác EFG vuông tại G (định lí Pythagore đảo).

Bài 3 trang 52 SBT Toán 8 Tập 1: Tính chiều cao BH của tam giác ABC cân tại B (Hình 5), biết AB = 9 cm và AC = 4 cm.

Lời giải:

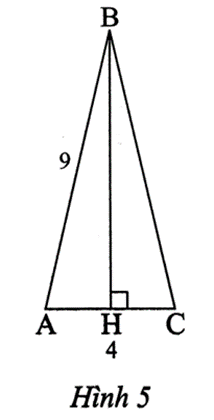
Tam giác ABC cân tại B nên đường cao BH cũng là đường trung tuyến.

Suy ra $AH=\frac{AC}{2}=\frac{4}{2}=2$ (cm)

Áp dụng định lí Pythagore vào tam giác ABH vuông tại H, ta có:

AB² = AH² + BH²

Suy ra BH² = AB² – AH² = 9² – 2² = 77.

Do đó $BH=\sqrt{77}$(cm).

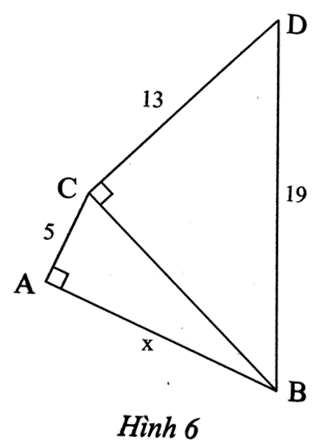
Bài 4 trang 52 SBT Toán 8 Tập 1: Tính độ dài x trong Hình 6.

Lời giải:

Áp dụng định lí Pythagore vào tam giác BCD vuông tại C, ta có:

BD² = BC² + CD²

Suy ra: BC² = BD² ‒ CD² = 19² ‒ 13² = 192.

Áp dụng định lí Pythagore vào tam giác ABC vuông tại A, ta có:

BC² = AB² + AC²

Suy ra: AB² = BC² ‒ AC² = 192 ‒ 5² = 167.

Do đó $AB=x=\sqrt{167}$ (cm).

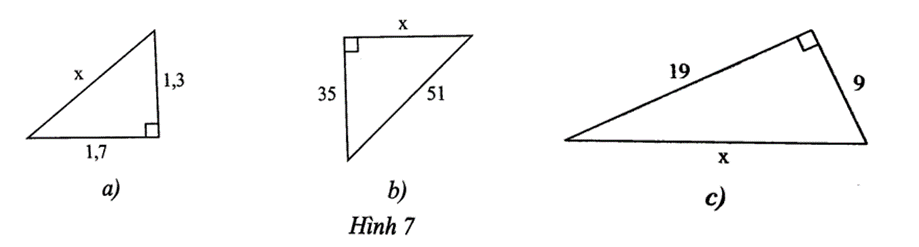
Bài 5 trang 52 SBT Toán 8 Tập 1: Tính độ dài các cạnh chưa biết của tam giác vuông sau:

Lời giải:

Áp dụng định lý Pythagore trong tam giác vuông ta có:

a) x² = 1,3² + 1,7² = 4,58

Suy ra: $x=\sqrt{4,58}\approx 2,1$.

b) 51² = 35² + x²

Suy ra x² = 51² – 35² = 1376.

Do đó $x=\sqrt{1376}\approx 37$.

c) x² = 19² + 9² = 442.

Suy ra $x=\sqrt{442}\approx 21$.

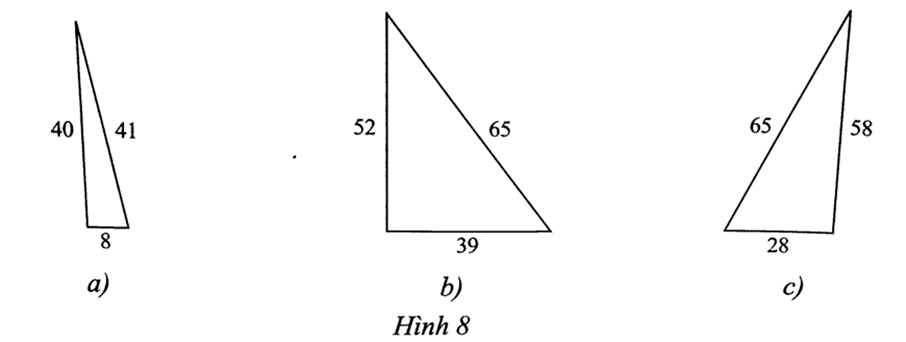
Bài 6 trang 52 SBT Toán 8 Tập 1: Tìm tam giác vuông trong các tam giác sau:

Lời giải:

a) Vì 41² = 1681 ≠ 1664 = 40² + 8² nên Hình 8a không là tam giác vuông.

b) Vì 65² = 4225 = 52² + 39² nên theo định lí Pythagore thì Hình 8b là tam giác vuông.

c) Vì 65² = 4225 ≠ 4148 = 58² + 28² nên Hình 8c không là tam giác vuông.

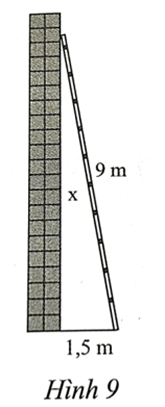
Bài 7 trang 53 SBT Toán 8 Tập 1: Tính khoảng cách x từ đầu thang đến chân tường (Hình 9).

Lời giải:

Khoảng cách x từ đầu thang đến chân tường bằng độ dài cạnh góc vuông trong tam giác vuông nên áp dụng định lý Pythagore trong tam giác vuông ta có:

9² = x² + 5², suy ra $x=\sqrt{9^2-1,5^2}\approx 8,9$ (m).

Bài 8 trang 53 SBT Toán 8 Tập 1: Một máy bay đang ở độ cao 5,2 km. Khoảng cách từ hình chiếu vuông góc của máy bay xuống mặt đất đến vị trí A của sân bay là 10,2 km (Hình 10). Tính khoảng cách từ vị trí máy bay đến vị trí A của sân bay.

Lời giải:

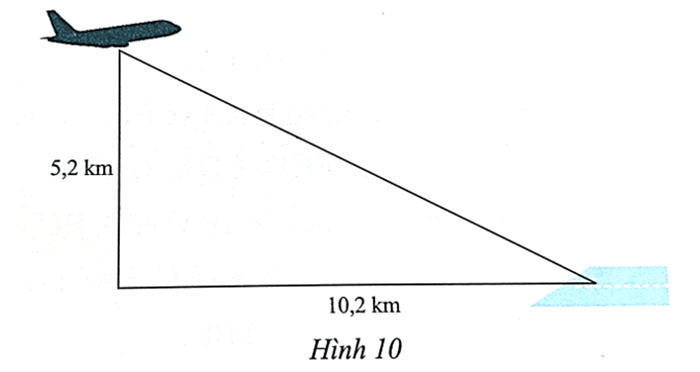
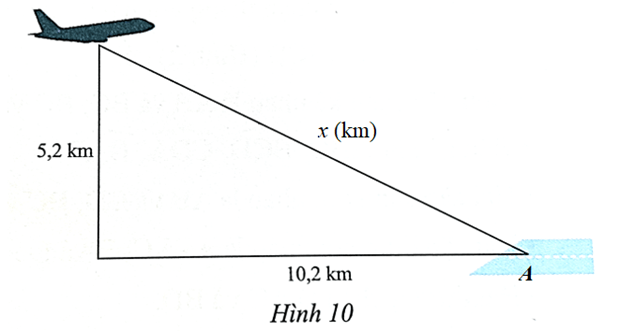
Gọi khoảng cách từ vị trí máy bay đến vị trí A của sân bay là x(km) (x > 0).

Khoảng cách từ vị trí máy bay đến vị trí A của sân bay là độ dài cạnh huyền trong tam giác vuông nên áp dụng định lý Pythagore trong tam giác vuông ta có:

x² = 5,2² + 10,2², suy ra $x=\sqrt{10,2^2+5,2^2}\approx 11,4$ (km).

Vậy khoảng cách từ vị trí máy bay đến vị trí A của sân bay là khoảng 11,4 km.

Xem thêm lời giải Sách bài tập Toán 8 bộ sách Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Diện tích xung quanh và thể tích của hình chóp tam giác đều, hình chóp tứ giác đều

Bài tập cuối chương 2 trang 44

Bài 2: Tứ giác

Bài 3: Hình thang – Hình thang cân

Bài 4: Hình bình hành – Hình thoi