Cho tứ diện OABC có OA = OB = OC = a, góc AOB= góc AOC= 60 độ và BOC= 90 độ . a) Chứng minh rằng (OBC)  (ABC).

Trả lời

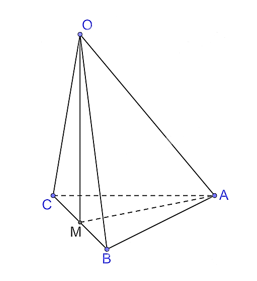
a) Gọi M là trung điểm của BC.

Xét tam giác OBC có OB = OC = a nên tam giác OBC cân tại O mà OM là trung tuyến nên OM đồng thời là đường cao hay OM ^ BC.

Vì tam giác OAC có OA = OC = a và $\widehat{AOC}=60°$  nên tam giác OAC đều, suy ra AC = a.

Vì tam giác OAB có OA = OB = a và $\widehat{AOB}=60°$  nên tam giác OAB đều, suy ra AB = a.

Xét tam giác OBC vuông tại O, có $BC=\sqrt{O{C}^2+O{B}^2}=\sqrt{a^2+a^2}=a\sqrt{2}$  .

Xét tam giác OBC vuông tại O, OM là đường cao, có

$\frac{1}{O{M}^2}=\frac{1}{O{B}^2}+\frac{1}{O{C}^2}=\frac{1}{a^2}+\frac{1}{a^2}=\frac{2}{a^2}\Rightarrow OM=\frac{a}{\sqrt{2}}$.

Vì BC² = 2a² = a² + a² = AB² + AC² nên tam giác ABC vuông tại A.

Mặt khác AB = AC nên tam giác ABC cân tại A có AM là trung tuyến nên AM đồng thời là đường cao hay AM ^ BC.

Xét tam giác ABC vuông tại A, AM là đường cao có:

$\frac{1}{A{M}^2}=\frac{1}{A{B}^2}+\frac{1}{A{C}^2}=\frac{1}{a^2}+\frac{1}{a^2}=\frac{2}{a^2}\Rightarrow AM=\frac{a}{\sqrt{2}}$.

Vì OA² = a² = $\frac{a^2}{2}+\frac{a^2}{2}$ = OM² + AM² nên tam giác OMA vuông tại M, suy ra OM ^ MA.

Vì OM ^ MA và OM ^ BC nên OM ^ (ABC) mà OM Ì (OBC), suy ra (OBC) ^ (ABC).