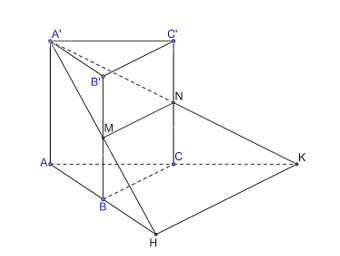
Cho hình lăng trụ tam giác đều ABC.A'B'C' có AB = a, $A{A}^{\text{'}}=a\sqrt{2}$  . Gọi M, N lần lượt là trung điểm của cạnh BB' và CC'. Mặt phẳng (A'MN) cắt đường thẳng AB, AC tương ứng tại H và K.

a) Chứng minh rằng MN // HK.

a) Vì M, N lần lượt là trung điểm của cạnh BB' và CC' nên MN // BC, suy ra MN // (ABC).

Mà (ABC) Ç (A'MN) = HK, suy ra MN // HK.