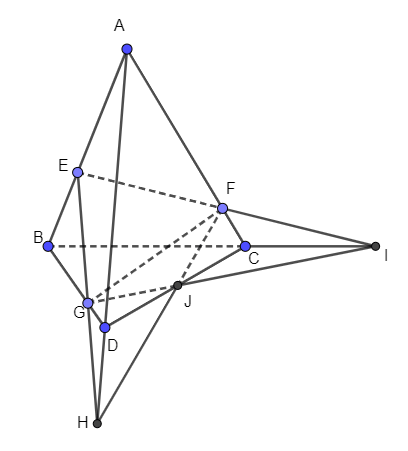
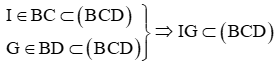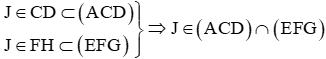Cho tứ diện ABCD. Gọi E, F, G lần lượt là ba điểm trên ba cạnh AB, AC, BD sao cho EF cắt BC tại I (I ≠ C), EG cắt AD tại H (H ≠ D)
4.3k
16/06/2023
Bài 4 trang 99 Toán 11 Tập 1: Cho tứ diện ABCD. Gọi E, F, G lần lượt là ba điểm trên ba cạnh AB, AC, BD sao cho EF cắt BC tại I (I ≠ C), EG cắt AD tại H (H ≠ D).
a) Tìm giao tuyến của các mặt phẳng (EFG) và (BCD), (EFG) và (ACD).
b) Chứng minh ba đường thẳng CD, IG, HF cùng đi qua một điểm.
Trả lời
a) +) Ta có: EF ∩ BC = {I}, EG ∩ BD = {G}
Mà EF, EG ⊂ (EGF) và BC, BD ⊂ (BCD)
Suy ra (EFG) ∩ (BCD) = {IG}.
+) Ta có: EF ∩ AC = {F}, EG ∩ AD = {H}
Mà EF, EG ⊂ (EGF) và AC, AD ⊂ (ACD)
Suy ra (EFG) ∩ (ACD) = {FH}.
b) Ta có: 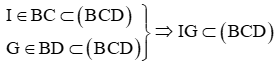
Mà CD ⊂ (BCD)
Gọi J là giao điểm của IG và CD.
Ta lại có: 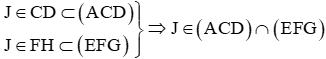
Mặt khác: (ACD) ∩ (EFG) = IG
Do đó J ∈ IG.
Vậy ba đường thẳng CD, IG, HF cùng đi qua điểm J.
Xem thêm các bài giải SGK Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Bài 3: Hàm số liên tục
Bài tập cuối chương 3
Bài 1: Điểm, đường thẳng và mặt phẳng trong không gian
Bài 2: Hai đường thẳng song song
Bài 3: Đường thẳng và mặt phẳng song song
Bài 4: Hai mặt phẳng song song