Cho tam giác ABC vuông cân tại A. Lấy điểm M thuộc cạnh huyền BC

Bài 25 trang 97 SBT Toán 8 Tập 1: Cho tam giác $ABC$ vuông cân tại $A$. Lấy điểm $M$ thuộc cạnh huyền $BC$. Gọi $D,E$ lần lượt là hình chiếu của điểm $M$ trên đường thẳng $AB,AC$.

Trả lời

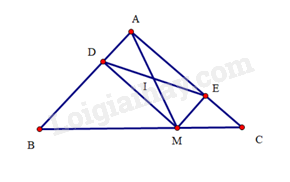
a) Tứ giác $ADME$ có $\widehat{DAE}=\widehat{AEM}=\widehat{MDA}={90}^{\circ }$ nên $ADME$ là hình chữ nhật.

b) Do $ADME$ là hình chữ nhật nên hai đường chéo $DE$ và $AM$ cắt nhau tại trung điểm của mỗi đường.

Mà $I$ là trung điểm của $DE$, suy ra $I$ là trung điểm của $AM$. Vậy ba điểm $A<I,M$ thẳng hàng.

c) Do $ADME$ là hình chữ nhật nên $DM//AC$. Suy ra $\widehat{BMD}=\widehat{ACB}$ (hai góc so le trong). Mà $\widehat{ABC}=\widehat{ACB}={45}^{\circ }$ (vì tam giác $ABC$ vuông cân tại $A$, suy ra $\widehat{BMD}=\widehat{ABC}={45}^{\circ }$. Do đó, tam giác $BDM$ cân tại $D$. Suy ra $BD=DM$.

Chu vi hình chữ nhật $ADME$ là: $2\left(AD+DM\right)=2\left(AD+BD\right)=DM$

Mà $AB$ không đổi nên chu vi của tứ giác $ADME$ không đổi.

d)     

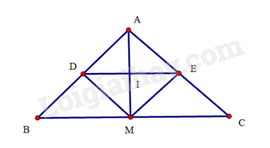
Do $ADME$ là hình chữ nhật nên $AM=DE$

Suy ra $DE$ có độ dài nhỏ nhất khi $AM$ có độ dài nhỏ nhất. vậy $M$ là hình chiếu của $A$ trên đường thẳng $BC$.

Trong tam giác $ABC$ vuông cân tại $A$ ta có

$AC=AB=2cm$ và $B{C}^2=A{B}^2+A{C}^2=8$

Suy ra $BC=\sqrt{8}cm$

$\mathrm{\Delta }ABM=\mathrm{\Delta }ACM$ (cạnh góc vuông – góc nhọn). Suy ra $BM=CM=\frac{BC}{2}=\sqrt{2}cm$

Tam giác $ABM$ vuông tại $M$ có $\widehat{ABM}={45}^{\circ }$ nên $\widehat{BAM}=\widehat{ABM}={45}^{\circ }$. Suy ra tam giác $ABM$ vuông cân tại $M$. Do đó $AM=BM=\sqrt{2}cm$. Vậy $DE=\sqrt{2}cm$.

Xem thêm các bài giải SBT Toán 8 Cánh diều hay, chi tiết khác:

Bài 3: Hình thang cân

Bài 4: Hình bình hành

Bài 5: Hình chữ nhật

Bài 6: Hình thoi

Bài 7: Hình vuông

Bài tập cuối chương 5 trang 103