Cho tam giác nhọn ABC. Gọi M, N, P lần lượt là trung điểm các cạnh AB, BC, CA và cho O là điểm
393
30/11/2023
Bài 2 trang 72 Toán 7 Tập 2:
Cho tam giác nhọn ABC. Gọi M, N, P lần lượt là trung điểm các cạnh AB, BC, CA và cho O là điểm cách đều ba đỉnh của tam giác ABC. Chứng minh rằng MO vuông góc với AB, NO vuông góc với BC và PO vuông góc với AC.
Trả lời
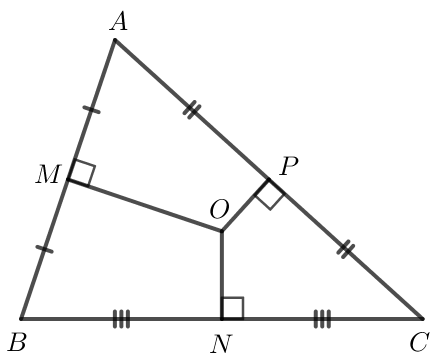
Điểm O là điểm cách đều ba đỉnh của tam giác ABC.
Suy ra O là giao điểm ba đường trung trực của tam giác ABC.
Khi đó do M, N, P lần lượt là trung điểm các cạnh AB, BC, CA nên MO AB, NO BC, PO AC.
Vậy MO vuông góc với AB, NO vuông góc với BC và PO vuông góc với AC.
Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:
Bài 4: Đường vuông góc và đường xiên
Bài 5: Đường trung trực của một đoạn thẳng
Bài 6: Tính chất ba đường trung trực của tam giác
Bài 7: Tính chất ba đường trung tuyến của tam giác
Bài 8: Tính chất ba đường cao của tam giác
Bài 9: Tính chất ba đường phân giác của tam giác

