Cho tam giác nhọn ABC có các đường cao AD, BE, CF. Chứng minh rằng:

a) ∆BDF ᔕ ∆BAC và ∆CDE ᔕ ∆CAB;

b) BF . BA + CE . CA = BC².

Lời giải

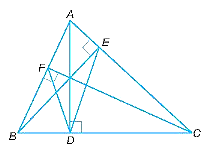
Vì AD, BE, CF là các đường cao của tam giác ABC nên AD vuông góc với BC, BE vuông góc với AC, CF vuông góc với AB.

Tam giác BDA vuông ở D và tam giác BFC vuông ở F có:

\(\widehat {ABC}\) chung.

Do đó, ∆BDA ᔕ ∆BFC (góc nhọn). Suy ra \(\frac{{BD}}{{BF}} = \frac{{BA}}{{BC}}\).

Suy ra \(\frac{{BD}}{{BA}} = \frac{{BF}}{{BC}}\).

Xét tam giác BDF và tam giác BAC có:

\(\frac{{BD}}{{BA}} = \frac{{BF}}{{BC}}\)

\(\widehat {ABC}\) chung

Do đó, ∆BDF ᔕ ∆BAC (c.g.c).

Tam giác CDA vuông ở D và tam giác CEB vuông ở E có:

\(\widehat {ACB}\) chung

Do đó, ∆CDA ᔕ ∆CEB (góc nhọn).

Nên \(\frac{{CD}}{{CE}} = \frac{{CA}}{{BC}}\).

Suy ra \(\frac{{CD}}{{CA}} = \frac{{CE}}{{BC}}\).

Tam giác CDE và tam giác CAB có:

\(\frac{{CD}}{{CA}} = \frac{{CE}}{{BC}}\)

\(\widehat {ACB}\) chung

Do đó, ∆CDE ᔕ ∆CAB (c.g.c).

b)

Theo chứng minh phần a ta có:

\(\frac{{BD}}{{BA}} = \frac{{BF}}{{BC}}\) nên BF . BA = BD . BC;

\(\frac{{CD}}{{CA}} = \frac{{CE}}{{BC}}\) nên CE . CA = CD . BC.

Suy ra BF . BA + CE . CA = BD . BC + CD . BC = BC.(BD + CD) = BC . BC = BC².

Vậy BF . BA + CE . CA = BC².