Cho ABC và A'B'C' lần lượt là các tam giác vuông tại đỉnh A và A'. Gọi M, M' lần lượt là trung điểm của AC và A'C'. Chứng minh rằng:

a) BC² + 3BA² = 4BM² và B'C'² + 3B'A'² = 4B'M'²;

b) Nếu $\frac{{BC}}{{BM}} = \frac{{B'C'}}{{B'M'}}$ thì ∆ABC ᔕ ∆A'B'C'.

Lời giải

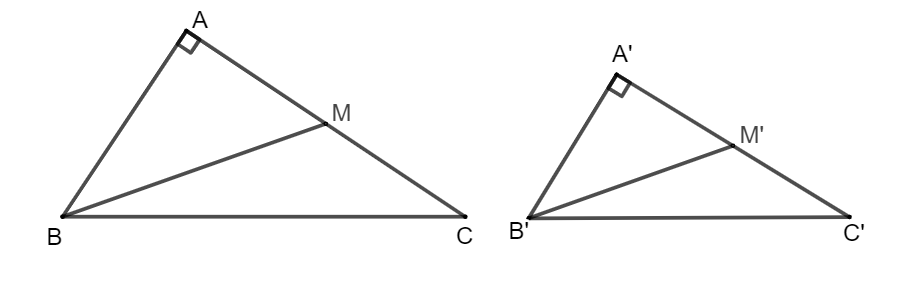
a) Vì M là trung điểm của AC nên AC = 2AM. Suy ra AC² = (2AM)² = 4AM².

Áp dụng định lý Pythagore cho tam giác ABC vuông tại A có:

BC² = AB² + AC².

Áp dụng định lý Pythagore cho tam giác ABM vuông tại A có:

BM² = AB² + AM².

Do đó, 4BM² = 4(AB² + AM²) = 4AB² + 4AM² = 4AB² + AC²

= 3AB² + (AB² + AC²) = 3AB² + BC².

Vậy BC² + 3BA² = 4BM².

Vì M' là trung điểm của A'C' nên A'C' = 2A'M'. Suy ra A'C'² = (2A'M')² = 4A'M'².

Áp dụng định lí Pythagore cho tam giác A'B'C' vuông tại A' có:

B'C'² = A'B'² + A'C'².

Áp dụng định lý Pythagore cho tam giác A'B'M' vuông tại A' có:

B'M'² = A'B'² + A'M'².

Do đó, 4B'M'² = 4(A'B'² + A'M'²) = 4A'B'² + 4A'M'²  = 4A'B'² + A'C'²

= 3A'B'² + (A'B'² + A'C'²) = 3A'B'² + B'C'².

Vậy B'C'² + 3B'A'² = 4B'M'².

b) Giả sử $\frac{{BC}}{{BM}} = \frac{{B'C'}}{{B'M'}}$. Suy ra $\frac{{B{C^2}}}{{B{M^2}}} = \frac{{B'C{'^2}}}{{B'M{'^2}}}$ (1).

Theo phần a ta có: BC² + 3BA² = 4BM², chia cả 2 vế cho BM², ta được:

$\frac{{B{C^2}}}{{B{M^2}}} + 3\frac{{B{A^2}}}{{B{M^2}}} = 4$.

Tương tự, ta có $\frac{{B'C{'^2}}}{{B'M{'^2}}} + 3\frac{{B'A{'^2}}}{{B'M{'^2}}} = 4$.

Do đó, $\frac{{B{C^2}}}{{B{M^2}}} + 3\frac{{B{A^2}}}{{B{M^2}}} = \frac{{B'C{'^2}}}{{B'M{'^2}}} + 3\frac{{B'A{'^2}}}{{B'M{'^2}}}\left( { = 4} \right)$      (2).

Từ (1) và (2), suy ra: $\frac{{B{A^2}}}{{B{M^2}}} = \frac{{B'A{'^2}}}{{B'M{'^2}}}$ hay $\frac{{BA}}{{BM}} = \frac{{B'A'}}{{B'M'}}$.

Do đó, $\frac{{BC}}{{B'C'}} = \frac{{BM}}{{B'M'}} = \frac{{BA}}{{B'A'}}$.

Hai tam giác ABC vuông tại A và A'B'C' vuông tại A' có $\frac{{BC}}{{B'C'}} = \frac{{BA}}{{B'A'}}$.

Vậy ∆ABC ᔕ ∆A'B'C' (ch – cgv).