Lời giải
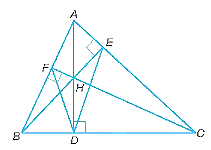
a)
Vì AD, BE, CF là các đường cao của tam giác ABC nên AD vuông góc với BC, BE vuông góc với AC, CF vuông góc với AB.
Tam giác AHE vuông ở H và tam giác BHD vuông ở D có:
\(\widehat {AHE} = \widehat {BHD}\) (hai góc đối đỉnh)
Do đó, ∆AHE ᔕ ∆BHD (góc nhọn).
Suy ra \(\frac{{AH}}{{BH}} = \frac{{HE}}{{HD}}\) nên HA . HD = HB . HE (1).
Tam giác HBF vuông ở F và tam giác HCE vuông ở E có:
\(\widehat {BHF} = \widehat {EHC}\) (hai góc đối đỉnh)
Do đó, ∆HBF ᔕ ∆HCE (góc nhọn).
Suy ra \(\frac{{HB}}{{HC}} = \frac{{HF}}{{HE}}\) nên HB . HE = HC . HF (2).
Từ (1) và (2) ta có: HA . HD = HB . HE = HC . HF.
b)
Tam giác AFC vuông ở F và tam giác AEB vuông ở E có:
\(\widehat {BAC}\) chung.
Do đó, ∆AFC ᔕ ∆AEB (góc nhọn)
Suy ra \(\frac{{AF}}{{AE}} = \frac{{AC}}{{AB}}\) nên AF . AB = AE . AC.
c)
Vì HA . HD = HB . HE nên \(\frac{{HA}}{{HE}} = \frac{{HB}}{{HD}}\)
Tam giác HAB và tam giác HED có:
\(\frac{{HA}}{{HE}} = \frac{{HB}}{{HD}}\) (cmt)
\(\widehat {AHB} = \widehat {EHD}\) (hai góc đối đỉnh)
Do đó, ∆AHB ᔕ ∆EHD (c.g.c).
Suy ra \(\widehat {HAB} = \widehat {HED}\).
Mà \(\widehat {HAB} + \widehat {FBD} = \widehat {HED} + \widehat {DEC}\) (= \(90^\circ \)).
Do đó, \(\widehat {FBD} = \widehat {DEC}\).
Chứng minh tương tự ta có: \(\widehat {BFD} = \widehat {ECD}\).
Tam giác BDF và tam giác EDC có:
\(\widehat {FBD} = \widehat {DEC}\) (cmt)
\(\widehat {BFD} = \widehat {ECD}\) (cmt)
Do đó, ∆BDF ᔕ ∆EDC (g.g).
Suy ra: \(\widehat {BDF} = \widehat {EDC}\).
Mà \[\widehat {BDF} + \widehat {FDH} = \widehat {EDC} + \widehat {HDE}\left( { = 90^\circ } \right)\].
Do đó, \(\widehat {FDH} = \widehat {HDE}\) hay \(\widehat {FDA} = \widehat {ADE}\).
Vậy DA là tia phân giác của góc EDF.

