Cho tam giác ABC vuông tại A có đường cao AH. Từ H kẻ đường thẳng HE vuông góc với AB (E thuộc AB). Chứng minh rằng:

a) ∆ABC ᔕ ∆HAC và CA² = CH . CB.

b) \(\frac{{AH}}{{BC}} = \frac{{HE}}{{AB}}\).

Lời giải

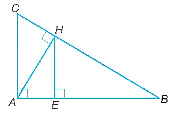
a) Vì AH là đường cao trong tam giác ABC nên AH vuông góc với BC.

Tam giác ABC vuông tại A và tam giác HAC vuông tại H có:

\(\widehat C\) chung

Do đó, ∆ABC ᔕ ∆HAC (góc nhọn).

Suy ra \(\frac{{AC}}{{HC}} = \frac{{BC}}{{AC}}\) nên AC² = CH . BC.

b)

Vì HE vuông góc với AB (E thuộc AB) nên \(\widehat {AEH} = 90^\circ \).

Ta có \(\widehat {HAE} + \widehat {CAH} = \widehat {CAB} = 90^\circ \) và \(\widehat C + \widehat {CAH} = 90^\circ \) (do tam giác CAH vuông tại H).

Do đó, \(\widehat {HAE} = \widehat C\) (cùng phụ với góc CAH).

Tam giác AHE vuông ở E và tam giác CBA vuông ở A có:

\(\widehat {HAE} = \widehat C\)

Do đó, ∆AHE ᔕ ∆CBA (hai góc nhọn bằng nhau).

Suy ra: \(\frac{{AH}}{{BC}} = \frac{{HE}}{{AB}}\).