Lời giải
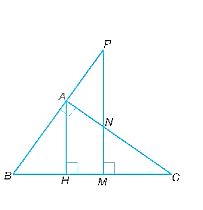
a) Vì tam giác ABC vuông tại A nên \(\widehat {BAC} = 90^\circ \).
Mà \(\widehat {BAC} + \widehat {PAN} = 180^\circ \) (hai góc kề bù)
Do đó, \(\widehat {PAN} = 90^\circ \).
Vì MN vuông góc với BC, AH vuông góc với BC nên MN song song với AH hay MP song song với AH.
Do đó, \(\widehat P = \widehat {HAB}\) (hai góc đồng vị).
Tam giác ANP vuông tại A và tam giác HBA vuông tại H có:
\(\widehat P = \widehat {HAB}\) (cmt)
Do đó, ∆ANP ᔕ ∆HBA (hai góc nhọn bằng nhau).
Tam giác MCN vuông tại M và tam giác MPB vuông tại M có:
\(\widehat C = \widehat P\) (cùng phụ với góc B).
Do đó, ∆MCN ᔕ ∆MPB (hai góc nhọn bằng nhau).
b)
Ta có: \(\frac{{MB}}{{MC}} \cdot \frac{{NC}}{{NA}} \cdot \frac{{PA}}{{PB}} = \frac{{MB}}{{PB}} \cdot \frac{{NC}}{{NA}} \cdot \frac{{PA}}{{MC}}\).
Tam giác PMB có: PM song song với AH nên theo định lí Thalès ta có:
\(\frac{{MB}}{{MH}} = \frac{{PB}}{{PA}}\) hay \(\frac{{MB}}{{PB}} = \frac{{MH}}{{PA}}\).
Tam giác AHC có: MN song song với AH nên theo định lí Thales ta có:
\(\frac{{NC}}{{NA}} = \frac{{MC}}{{MH}}\).
Do đó, \(\frac{{MB}}{{MC}} \cdot \frac{{NC}}{{NA}} \cdot \frac{{PA}}{{PB}} = \frac{{MB}}{{PB}} \cdot \frac{{NC}}{{NA}} \cdot \frac{{PA}}{{MC}}\)\( = \frac{{MH}}{{PA}} \cdot \frac{{MC}}{{MH}} \cdot \frac{{PA}}{{MC}} = 1\).

