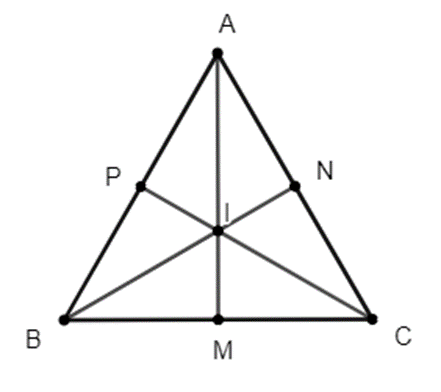
Gọi M, N, P lần lượt là hình chiếu của I trên BC, AC, AB.

Khi đó IM = IN = IP.

+) Chứng minh I cách đều ba đỉnh của tam giác ABC.

Xét ∆AIP và ∆AIN có:

\(\widehat {API} = \widehat {AQI} = 90^\circ \)

AI là cạnh chung,

IP = IN (cmt)

Do đó ∆AIP = ∆AIN (cạnh huyền – cạnh góc vuông)

Suy ra AP = AN (hai cạnh tương ứng) và \(\widehat {PAI} = \widehat {NAI}\) (hai góc tương ứng)

 Do đó AI là tia phân giác của góc BAC.

Mà \(\widehat {BAC} = 60^\circ \) (do tam giác ABC đều).

Nên \(\widehat {PAI} = \widehat {NAI} = 30^\circ \)

Xét ∆API vuông tại P có:

\(\widehat {PAI} + \widehat {PIA} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°).

Suy ra \(\widehat {PIA} = 90^\circ - \widehat {PAI} = 90^\circ - 30^\circ = 60^\circ \)

Chứng minh tương tự ta có: \(\widehat {PIB} = 60^\circ \)

Xét ∆PIA và ∆PIB có:

\(\widehat {API} = \widehat {BPI} = 90^\circ \)

PI là cạnh chung

\(\widehat {PIA} = \widehat {PIB}\) (cùng bằng 60°)

Do đó ∆PIA = ∆PIB (cạnh góc vuông – góc nhọn kề).

Suy ra IA = IB (hai cạnh tương ứng)

Chứng minh tương tự ta cũng có IB = IC.

Do đó IA = IB = IC nên I cách đều ba đỉnh của tam giác ABC.