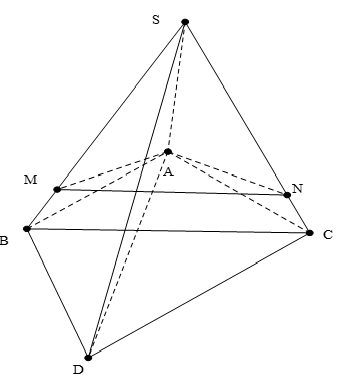
Cho tam giác ABC có BC=a, $\widehat{BAC}={135}^0$. Trên đường thẳng vuông góc với (ABC) tai A lấy điểm S thỏa mãn $SA=a\sqrt{2}$. Hình chiếu vuông góc của A trên SB, SC lần lượt là M,N. Góc giữa hai mặt phẳng $\left(ABC\right)$ và $\left(AMN\right)$ là?

Chọn C

Trong mặt phẳng $\left(ABC\right)$ lấy điểm D sao cho $\widehat{DBA}=\widehat{DCA}=90°$.

Dễ thấy $DC\perp \left(SAC\right)\Rightarrow DC\perp AN$lại có $AN\perp SC\Rightarrow AN\perp \left(SCD\right)\Rightarrow AN\perp SD$.

Tương tự $AM\perp SD\Rightarrow SD\perp \left(AMN\right)$.

Ta có tứ giác ABCD nội tiếp đường tròn đường kính AD.

$\Rightarrow AD=2.R=\frac{BC}{\sin \widehat{BAC}}=a\sqrt{2}\Rightarrow \Delta SAD$vuông cân tại $A\Rightarrow \widehat{DSA}=45°$.

Mà $SA\perp \left(ABC\right)$và $SD\perp \left(AMN\right)\Rightarrow$ góc giữa hai mặt phẳng $$$\left(ABC\right)$ và $$$\left(AMN\right)$ là góc giữa SA và SD và bằng $45°$.