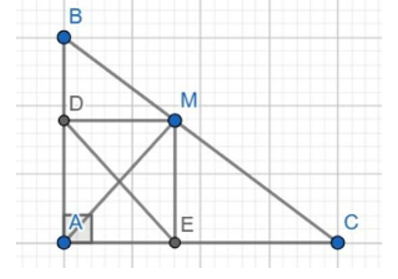
Cho tam giác ABC vuông tại A. Từ điểm M bất kì trên cạnh BC ( M không trùng với BC )

Trả lời

a)

Ta có: $\text{MD//AC, AB}\perp \text{AC}\left(gt\right)$

_{$\Rightarrow \text{MD}\perp \text{AB}$}

Tương tự $\Rightarrow ME\perp AC$

Xét tứ giác ADME:

$\begin{array}{l}\widehat{\text{DAE}}{\text{ = 90}}^{\text{o}}\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}(AB}\perp \text{AC)}\\ \text{}\widehat{\text{ADM}}{\text{ = 90}}^{\text{o}}\text{\hspace{0.17em}\hspace{0.17em}(MD}\perp \text{AB)}\\ \text{}\widehat{\text{AEM}}{\text{ = 90}}^{\text{o}}\text{\hspace{0.17em}\hspace{0.17em}(ME}\perp \text{AC)}\end{array}$

→ Tứ giác ADME là hình chữ nhật (tứ giác có 3 góc vuông)

→ AD = ME, DM = AE

b)

Ta có: AD = ME = 3cm, DM = AE = 4cm

${\text{AD}}^{\text{2}}{\text{ + DM}}^{\text{2}}{\text{ = AM}}^{\text{2}}$

$\Delta DME$ vuông tại D:

$\Rightarrow {\text{S}}_{\text{VDME}}\text{ = }\frac{\text{1}}{\text{2}}\text{.DM.ME = }\frac{\text{1}}{\text{2}}{\text{.4.3 = 6(cm}}^{\text{2}}\text{)}$(định lý Pytago)

$\Delta DME$ vuông tại M

$\Rightarrow {\text{S}}_{\text{VDME}}\text{ = }\frac{\text{1}}{\text{2}}\text{.DM.ME = }\frac{\text{1}}{\text{2}}{\text{.4.3 = 6(cm}}^{\text{2}}\text{)}$