Cho tam giác ABC vuông tại A có đường cao AH chia cạnh huyền BC thành 2 đoạn

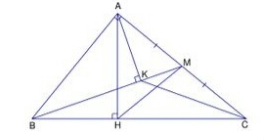
Đề bài: Cho tam giác ABC vuông tại A có đường cao AH chia cạnh huyền BC thành 2 đoạn: BH = 4cm và HC = 6cm.
a) Tính độ dài các đoạn AH, AB, AC
b) Gọi M là trung điểm của AC. Tính số đó góc AMB (làm tròn đến độ)
c) Kẻ AK vuông góc BM (K thuộc BM). Chứng minh: $\frac{BK}{BH}=\frac{BC}{BM}$

Trả lời

Hướng dẫn giải:

A_ Tính độ dài các đoạn AH, AB, AC

∆ABC vuông tại A:

+ $A{H}^2=HB.HC=4.6=24\Rightarrow AH=2\sqrt{6}\left(cm\right)$

+ $A{B}^2=BC.HB=10.4=40\Rightarrow AB=2\sqrt{10}\left(cm\right)$

+ $A{C}^2=BC.HC=10.6=60\Rightarrow AC=2\sqrt{15}\left(cm\right)$

b) Gọi M là trung điểm của AC. Tính số đo góc AMB (làm tròn độ). ∆ABM vuông tại A

$tgAMB=\frac{AB}{AM}=\frac{2\sqrt{10}}{\sqrt{15}}=\frac{2\sqrt{6}}{3}\Rightarrow AMB\approx 59°$

c) Kẻ AK vuông góc với BM ( $K\in BM$ ). Chứng minh: $\Delta BKC~\Delta BHM$

∆ABM vuông tại A có: $AK\perp BM$

+ AB² = BK.BM

∆ABC vuông tại A có: $AH\perp BC$

+ AB² = BH.BC

$\Rightarrow BK.BM=BH.BC$ hay $\frac{BK}{BH}=\frac{BC}{BM}$