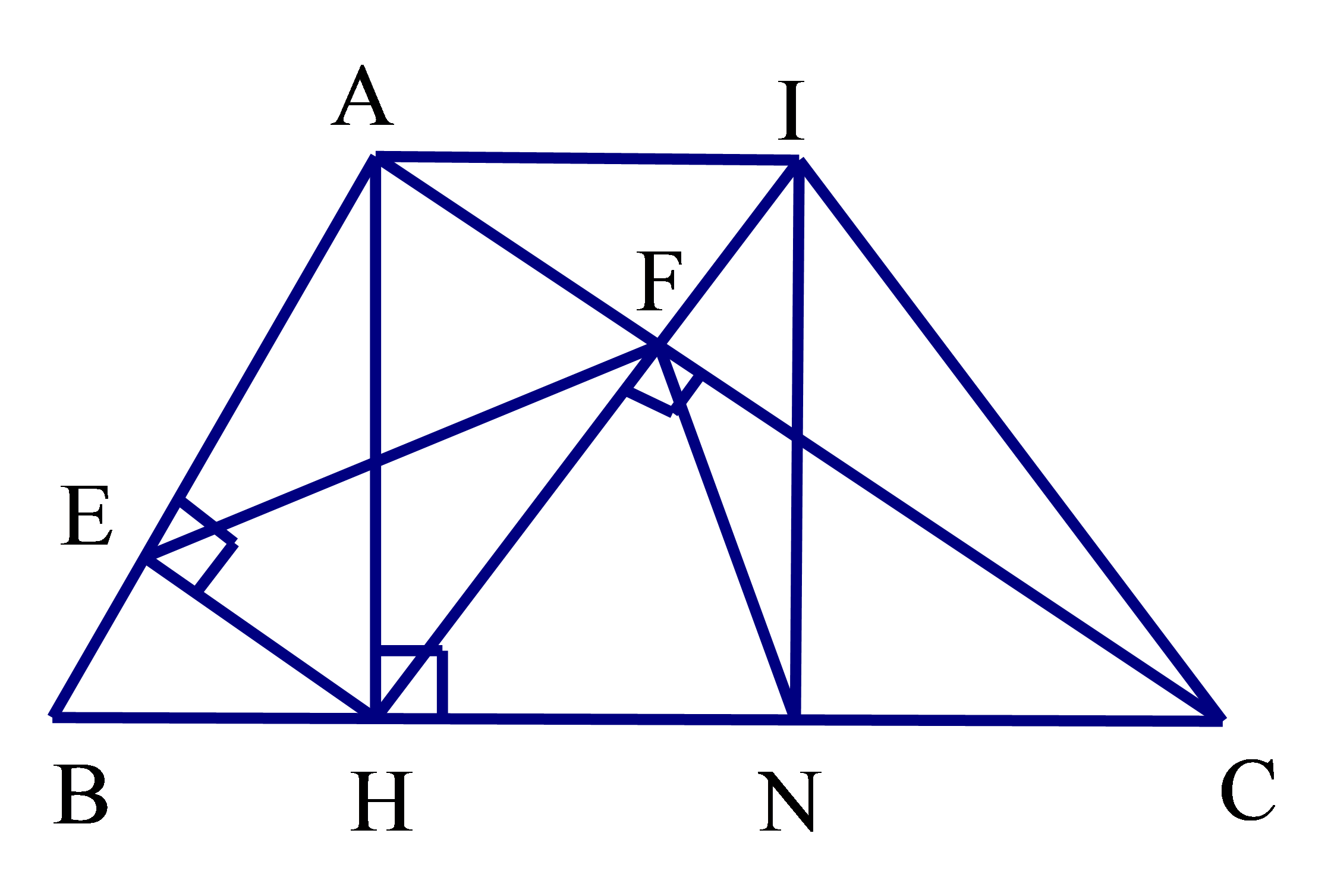
Cho tam giác ABC vuông tại A (AB < AC). Kẻ đường cao AH (H ∈ BC). a) Chứng minh rằng ΔABH ᔕ ΔCBA, suy ra AB^2 = BH.BC. b) Vẽ HE vuông góc với AB tại E, vẽ HF vuông góc với AC tại F. Chứng m
Cho tam giác ABC vuông tại A (AB < AC). Kẻ đường cao AH (H ∈ BC).
a) Chứng minh rằng ΔABH ᔕ ΔCBA, suy ra AB2 = BH.BC.
b) Vẽ HE vuông góc với AB tại E, vẽ HF vuông góc với AC tại F. Chứng minh rằng AE.AB = AF.AC.
c) Chứng minh rằng ΔAFE ᔕ ΔABC.
d) Qua A vẽ đường thẳng song song với BC cắt đường thẳng HF tại I. Vẽ IN vuông góc BC tại N. Chứng minh rằng ΔHNF ᔕ ΔHIC.